参考材料
- Transformer vs CNN vs RNN 时间复杂度比较
- Attention is All You Need
- Transformer/CNN/RNN的对比(时间复杂度,序列操作数,最大路径长度)
- self-attention RNN CNN时间复杂度
说在前面
本篇文章仅仅是为了解释这三者的复杂度比较,而对比结构等问题不做比较
n:输入序列长度
d:embedding的大小
正文
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Self-Attention | O(n^2 · d) | O(1) | O(1) |
| Recurrent | O(n · d^2) | O(n) | O(n) |
| Convolutional | O(k · n · d^2) | O(1) | O(log_k(n)) |
| Self-Attention (restricted) | O(r · n · d) | O(1) | O(n/r) |
Complexity per Layer
Transformer:
说在前面:对于矩阵乘法的时间复杂度计算=行 x 列 x 共享维度
n×d的矩阵Q和 d×n的矩阵KT相乘的时间复杂度 为 O(n^2 d)
n×n的矩阵softamx(Q*KT)和 n×d的矩阵V相乘的时间复杂度 为 O(n^2 d)
而softmax(n×n)的时间复杂度为 O(n^2)
所以self-attention最终的时间复杂度为 O(n^2 d)(选最大的)
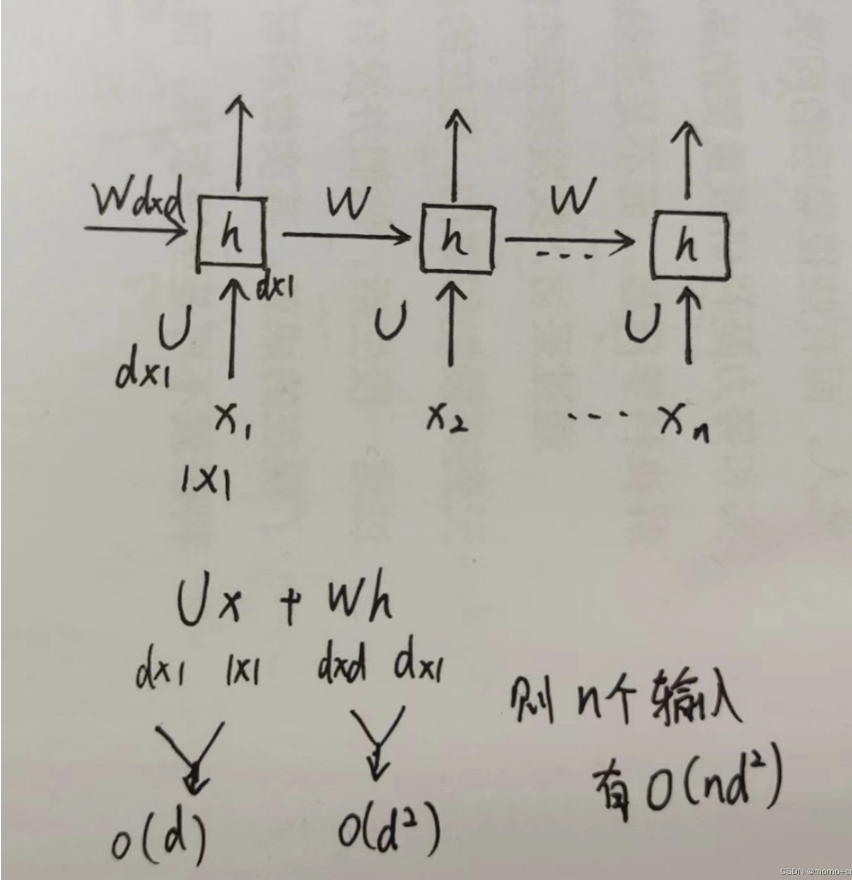
RNN:
考虑到矩阵(维度为𝑛 x 𝑛)和输入向量相乘,因此RNN每层计算复杂度为𝑂(𝑛 x 𝑑^2)
CNN:
注:这里保证估计输入输出都是一样的,即均为 n × d
需要对输入进行padding操作,因为这里kernel size为 k,(实际kernel的形状为 k × d)如果不padding的话,那么输出的每一个维度为 n − k + 1,因为这里stride是为1的。对于保证估计输入输出相同,则需要对序列的前后分别padding长度为 (k − 1) / 2。
大小为 k × d 的卷积核在一次运算的复杂度是: O(kd),这里直接理解为一维卷积
一共做了 n 次(每个数据都要卷积,所以是n次),故复杂度为 O(nkd)
对于证估计一维维度在每一个维度都相同,故需要 d 个卷积核 (输出通道数=卷积核个数) ,所以总体来看操作是的时间复杂度为 O(nkd²)
Sequential Operations
表明三种模型的并行程度:从计算方式上看,只有RNN才需要串行地完成
次序列操作,而self-attention和convolution (因为我们计算是按顺序计算的,但是实际计算机计算是可以并行计算的) 的n次序列操作均可以并行完成。因为RNN还需要依赖于上一个时间步的隐藏层输出,而其他模型仅仅依赖于输入。
Maximum Path Length
RNN:
长度为 n的序列中,节点之间的最大路径长度为n,即o(n)。第一个token的信息需要经过n次迭代才能传到最后一个时间步的状态中,信息丢失严重,很难建立节点间的长距离依赖。
CNN:
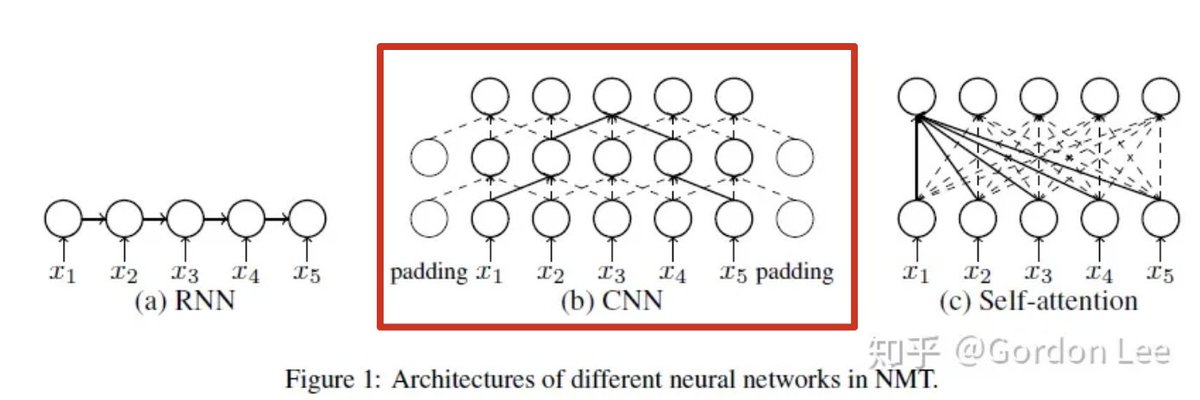
通过convolution layer来逐渐扩大感知域,扩大感知域可以理解为增大每个“看到”的local context的大小/取值区间的能力。在一次卷积操作中,感知域L的CNN中,能看到最大的local context的大小/取值区间 L(k − 1) + 1,最大增长长度为
例如图(b)中是一个两层的卷积核大小为3的CNN,顶层节点能看到的最大local context为2*2+1=5个token的范围。根据这样,上图可以得出一个 k 大小,深度为 h 的树,叶子节点总数为 = n,解得最大深度树的深度 h = ,即 O()
Transformer:
Self-attention: 任意两个位置都可以直接相连,即任意两个位置之间的距离为1
受限的self-attention: 类似于考虑大小为 r 的CNN, 最大路径长度为 O(n/r)