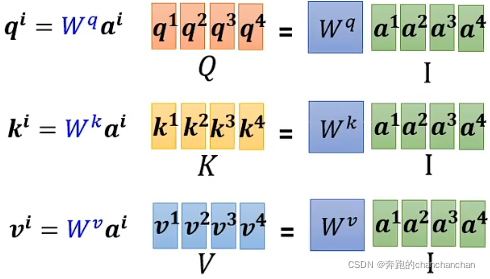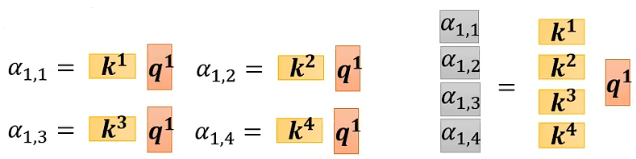paper:Transformer

参考链接

1.abstract

主流的序列转换模型都是基于复杂的循环或卷积神经网络，我们的模型包含一个编码器和一个解码器。具有最好性能的模型在编码和解码之间通过一个注意力机制链接编解码器。我们提出了一个新的简单网络结构——Transformer，其仅仅是基于注意力机制，而完全不需要之前的循环或卷积。在两个机器翻译任务上的实验表明，该模型具有更好的性能，同时并行度更好，并且训练时间更少。（泛化到其它任务效果也不错）

1
2
3

在WMT 2014英语到德语翻译任务上，我们的模型达到了28.4 BLEU，比之前最好的结果提高了2 BLEU。在WMT 2014英语到法语翻译任务上，我们的模型在8个GPU上训练3.5天后，所得到的单个模型获得了41.8 BLEU分数。我们在大型和有限的训练数据中，通过将其成功应用于英语句法解析，表明了Transformer可以很好地适用于其他任务。

可以看到这篇文章最开始只是针对机器翻译来写的，transformer在机器翻译上效果也很好。但是随着bert、GPT等把这种架构用在更多的NLP任务上，甚至后面CV和video等也可以使用注意力机制，整个工作就火出圈了。

2.结论

本文介绍了Transformer，这是第一个完全基于注意力的序列转换模型，用多头自注意力（multi-headed self-attention）代替了 encoder-decoder 架构中最常用的循环层。

对于翻译任务，Transformer可以比基于循环或卷积层的体系结构训练更快。在WMT 2014 English-to-German和 WMT 2014 English-to-French翻译任务中，我们取得了最好的结果。在前面的任务中，我们最好的模型甚至胜过以前发表过的所有整合模型。

我们对基于注意力的模型的未来感到兴奋，并计划将Transformer应用于文本之外的涉及输入和输出模式的问题中任务，以有效处理大型输入&输出任务，如图像、音频和视频等,让生成不那么时序化是我们的另一个研究目标。

我们用于训练和评估模型的代码可以在https://github.com/tensorflow/tensor2tensor上获得。

3.导论

序列建模和转换问题（如机器翻译）最新方法是LSTM和GRN等。后面许多研究都围绕循环语言模型和编码器-解码器体系结构进行。

循环网络模型通常是考虑了输入和输出序列的中字符位置的计算。当前时刻隐藏状态ht，是由上一时刻隐藏状态ht−1和 t时刻输入共同决定的。（把之前的信息都放在隐藏状态里，一个个传递下去，是RNN处理时序信息的关键）。这种固有的时序模型难以并行化处理，计算性能就很差。这些年做了一些并行化改进，但是问题依然存在。

另外还存在长距离衰减问题，解码阶段，越靠后的内容，翻译效果越差。除非你把ht维度设置的很高，可以把每一个时间步的信息都存下来。但这样会造成内存开销很大。

attention在此之前，已经成功的应用在encoder-decoder 架构中，但主要是用在如何把编码器的信息有效的传递给解码器，所以是和RNN一起使用的。

本文提出的Transformer，不再使用循环神经层，而是纯基于注意力机制，来构造输入和输出之间的全局依赖关系。Transformer可以进行更多的并行化，训练时间更短但翻译效果更好。

4. 背景

使用卷积神经网络替换循环神经网络，并行计算所有输入和输出位置的隐藏表示，是扩展神经GPU，ByteNet和ConvS2S的基础，因为这样可以减少时序计算。但是CNN对长序列难以建模（因为卷积计算时，卷积核/感受野比较小，如果序列很长，需要使用多层卷积才可以将两个比较远的位置关联起来）。但是使用Transformer的注意力机制的话，每次（一层）就能看到序列中所有的位置，就不存在这个问题。

关联来自两个任意输入或输出位置的数据所需的操作数量，随着距离增长，对于ConvS2S呈线性，对于ByteNet呈对数，而对于Transformer是常数，因为一次就看到了。

但是卷积的好处是，输出可以有多个通道，每个通道可以认为是识别不同的模式，作者也想得到这种多通道输出的效果，所以提出了Multi-Head Attention多头注意力机制。（模拟卷积多通道输出效果）

Self-attention，有时称为intra-attention，是一种关联单个序列的不同位置以计算序列表示的关联机制。在此之前已成功用于多种任务。但据我们所知，Transformer是第一个完全依靠self-attention，而不使用卷积或循环的的encoder-decoder 转换模型。

5. 模型架构

大部分神经序列转换模型都使用encoder-decoder结构。编码器将一个输入序列(x1, ..., xn)映射到一个连续的表示z = (z1, ..., zn)中。解码器根据z中的每个元素，逐步生成输出序列(y1, ..., ym)，每个时间步生成一个元素。在每一步中，模型都是自回归的，在生成下一个结果时，会将先前生成的结果作为当前的输入。

编码器和解码器的序列可以不一样长，且编码器可以一次性看到整个序列，但解码器是逐步输出的。

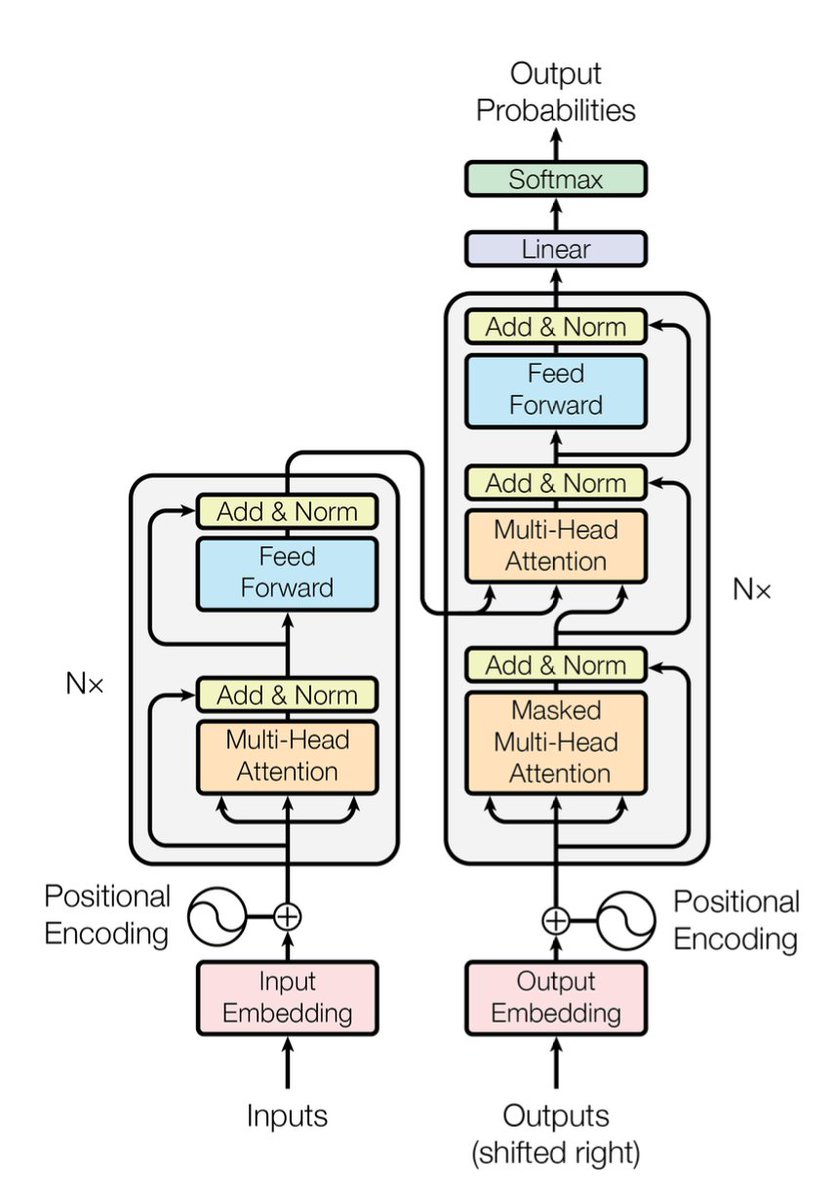
Transformer遵循这种整体架构，但对编码器和解码器使用堆叠的自注意力和逐点全连接层，如下图所示:

Outputs（shifted right）：解码器在初始时刻实际上没有输入，它的输入是编码器的输出。所以这里的"Outputs"表示输出序列，"shifted right"是指序列逐个右移的意思。
Nx：表示模块堆叠了N次。

图画得好，一张图能搞定所有东西，所以画图是一个基础技能。

5.1 Encoder

编码器由N=6个相同的encoder层堆叠组成。每层有两个子层：

multi-head self-attention
FFNN层（前馈神经网络层，Feed Forward Neural Network），实际上是MLP（多层感知器），为了更加专业，名称被设置得较长。每个子层都使用以下特点：
- 残差连接(residual connection) 后进行层归一化（layer normalization）。
- 每个子层的输出是LayerNorm(x + Sublayer(x))，其中Sublayer(x)是当前子层的输出。
- 为简化模型，所有子层以及嵌入层的向量维度都是d_model = 512。如果输入输出维度不一样，残差连接会进行投影以映射到统一维度。这种做法不同于传统的CNN或MLP，它们通常会进行一些下采样。

1	这种各层统一维度使得模型结构相对简单，只有`N`和`d_model`这两个参数需要调整。这个设计也影响到后面一系列的网络发展，如BERT和GPT等。

5.2 Decoder

解码器：解码器同样由 N=6个相同的decoder层堆栈组成，每个层有三个子层。

Masked multi-head self-attention：在解码器里，Self Attention 层只允许关注到输出序列中早于当前位置之前的单词。具体做法是：在 Self Attention 分数经过 Softmax 层之前，使用attention mask，屏蔽当前位置之后的那些位置。所以叫Masked multi-head self Attention。（对应masked位置使用一个很大的负数-inf，使得softmax之后其对应值为0）
Encoder-Decoder Attention ：编码器输出最终向量，将会输入到每个解码器的Encoder-Decoder Attention层，用来帮解码器把注意力集中中输入序列的合适位置。
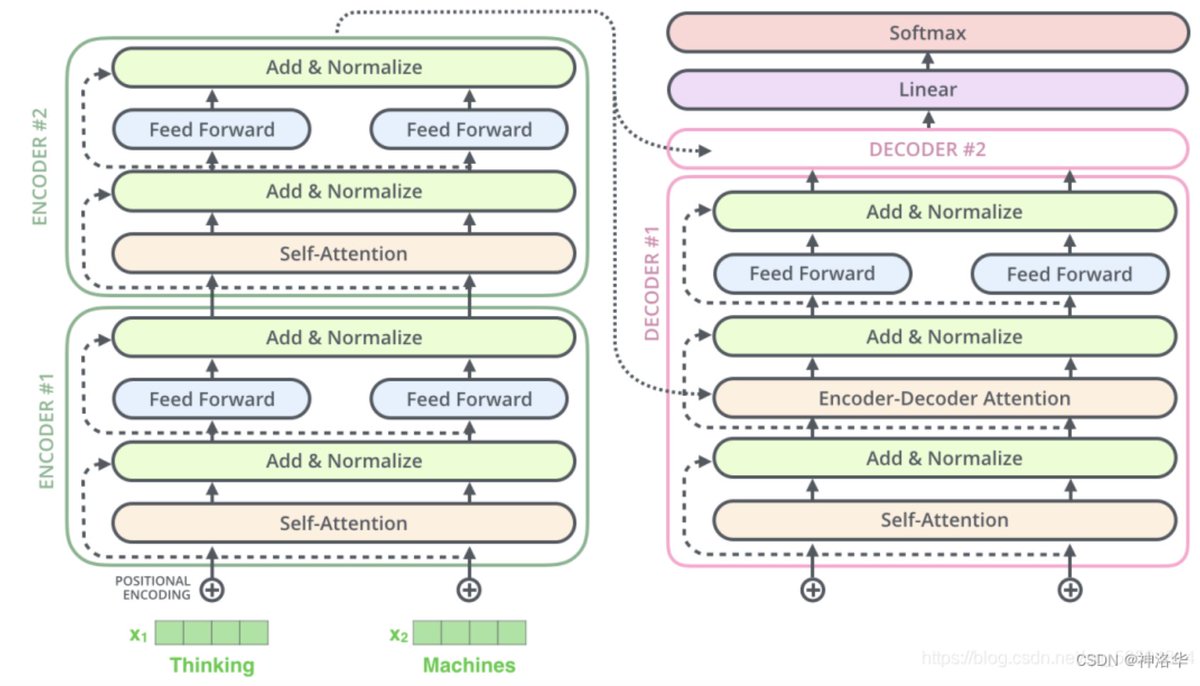
FFNN: 与编码器类似，每个子层都使用残差连接，然后进行层归一化。假设一个 Transformer 是由 2 层编码器和两层解码器组成的

5.3 LN VS BN

参考该文章：Normalization

5.4 Attention机制

attention函数可以被描述为将query和一组key-value对映射到输出，其中query、key、value和输出都是向量。输出被计算为value的加权求和，所以输出和value的维度一致。每个value的权重由query与对应key计算所得。（不同注意力机制有不同的算法）

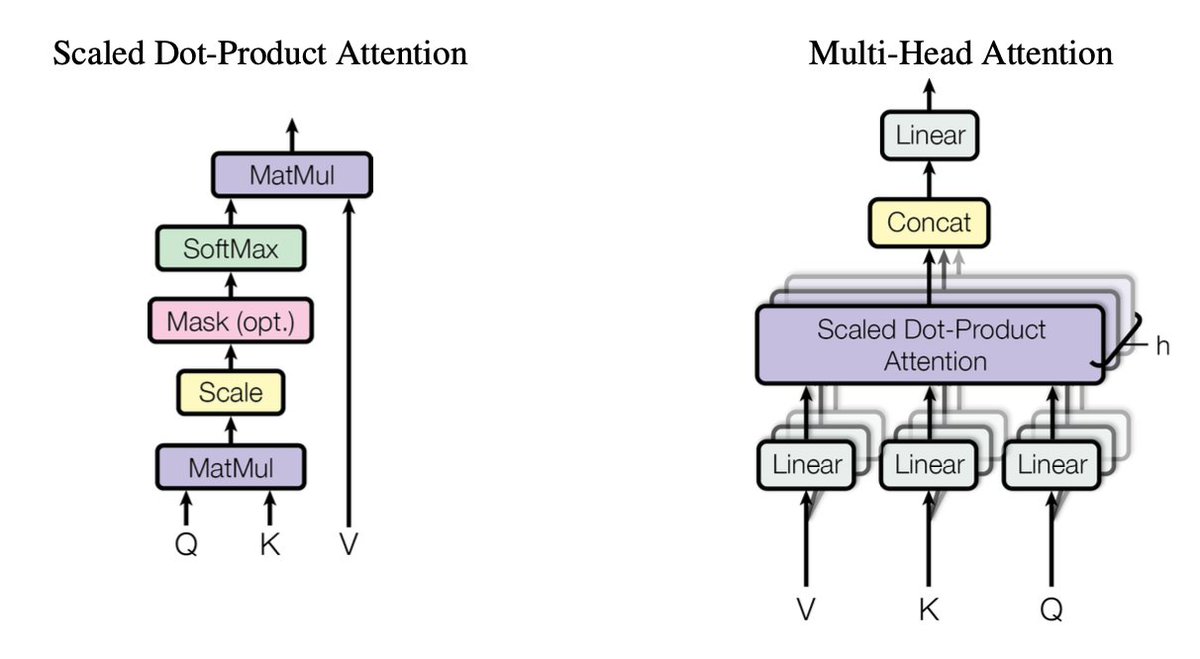
5.4.1 缩放的点积注意力（Scaled Dot-Product Attention）

缩放的点积注意力:

其输入为query、key(维度是 $d_k$ )以及values(维度是 $d_v$ )
计算query和所有key的点积,得到两个向量的相似度(结果越大相似度越高);然后对每个点积结果除以 $\sqrt{d_k}$
点积结果输入softmax函数获得value的权重。最后对value进行加权求和。

在实践中,我们同时计算一组query的attention函数,并将它们组合成一个矩阵Q。key和value也一起组成矩阵K和V。我们计算的输出矩阵为:

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

注意： K、V矩阵的序列长度是一样的(加权求和),而Q矩阵的序列长度可以和前两者不一样;这种情况发生在:解码器部分的Encoder-Decoder Attention层中,Q矩阵是来自解码器输出tgt,而K、V矩阵则是来自编码器最后的输出memory。即tgt2 = self.multihead_attn(tgt, memory,memory, attn_mask=memory_mask,key_padding_mask=memory_key_padding_mask)[0]。

但是Q和K的维度必须一样,因为要计算点积。

有两个最常用的attention函数:

1. 加法attention (cite):

$s = A^T \text{Tanh}(qW + kU)$

使用具有单个隐层的前馈网络计算,`q`和`k`维度不一致也可以进行;

2. 点积(乘法)attention:

除了缩放因子 $\frac{1}{\sqrt{d_k}}$ 之外,点积Attention跟我们的算法一样(所以作者的注意力叫缩放点积注意力)。虽然理论上点积attention和加法attention复杂度相似,但在实践中,点积attention可以使用高度优化的矩阵乘法来实现,因此点积attention计算更快、更节省空间。

当 $d_k$ 的值比较小的时候,这两个机制的性能相差相近,当 $d_k$ 比较大时,加法attention比不带缩放的点积attention性能好。我们怀疑,维度 $d_k$ 很大时,点积结果也变得很大,将softmax函数推向具有极小梯度的区域。为了抵消这种影响,我们将点积缩小 $\frac{1}{\sqrt{d\_k}}$ 倍。

5.4.2 多头注意力

多头注意力的定义如下:

$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O$

$\text{where} \ \text{head}_i = \text{Attention}(QW^Q_i, KW^K_i, VW^V_i)$

其中映射由权重矩阵完成: $W^Q_i \in \mathbb{R}^{d_{\text{model}} \times d_k}$ , $W^K_i \in \mathbb{R}^{d_{\text{model}} \times d_k}$ , $W^V_i \in \mathbb{R}^{d_{\text{model}} \times d_v}$ and $W^O \in \mathbb{R}^{hd_v \times d_{\text{model}}}$ 。

我们采用 $h = 8$ 个平行attention层或者叫head。对于这些head中的每一个,我们使用 $d_k = d_v = d_{\text{model}}/h = 64$ ,总计算成本与具有全部维度的单个head attention相似。

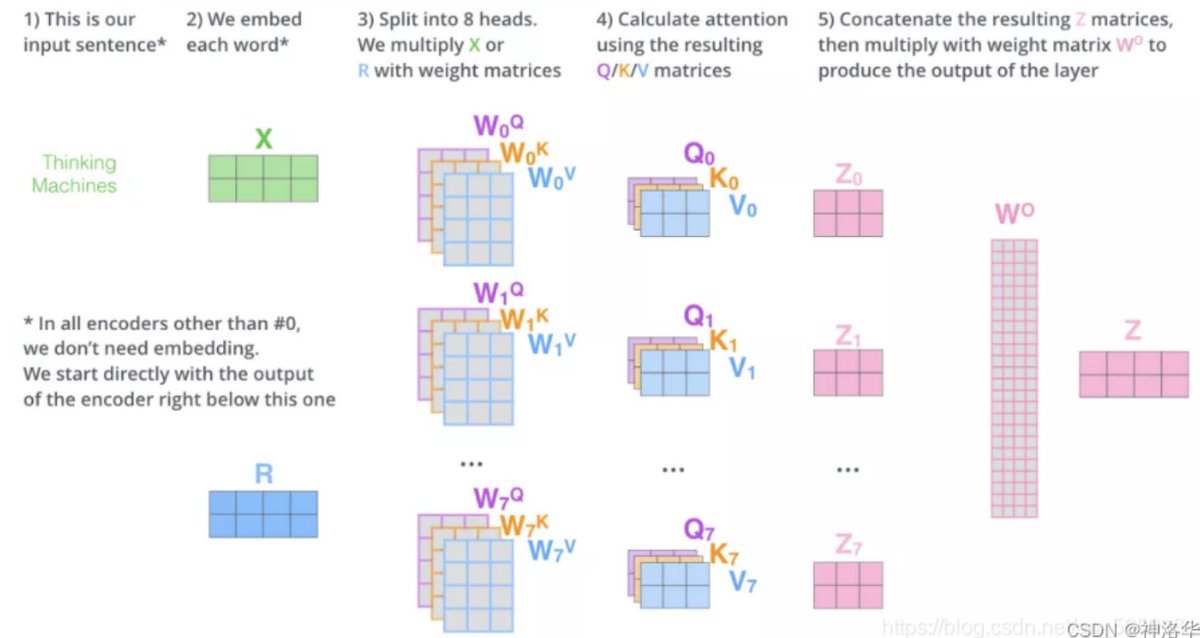
输入 $(X)$ 和8组权重矩阵 $W^Q$ , $W^K$ , $W^V$ 相乘,得到 8 组 $(Q)$ , $(K)$ , $(V)$ 矩阵。进行attention计算,得到 8 组 $(Z)$ 矩阵(假设head=8)。把8组矩阵拼接起来,乘以权重矩阵 $W^O$ ,将其映射回 $d$ 维向量(相当于多维特征进行汇聚),得到最终的矩阵 $(Z)$ 。这个矩阵包含了所有 attention heads(注意力头)的信息。矩阵 $Z$ 会输入到 FFNN层(前馈神经网络层接收的也是 1 个矩阵,而不是8个。其中每行的向量表示一个词)。

使用多头自注意力的好处:

多语义匹配:本身缩放点积注意力是没什么参数可以学习的,就是计算点积、softmax、加权和而已。但是使用Multi-head attention之后,投影到低维的权重矩阵 $W^Q$ , $W^K$ , $W^V$ 是可以学习的,而且有 $h=8$ 次学习机会。使得模型可以在不同语义空间下学到不同的的语义表示,也扩展了模型关注不同位置的能力。类似卷积中多通道的感觉。

例如, “小明养了一只猫,它特别调皮可爱,他非常喜欢它”。“猫”从指代的角度看,与“它”的匹配度最高,但从属性的角度看,与“调皮”“可爱”的匹配度最高。标准的 Attention 模型无法处理这种多语义的情况。
注意力结果互斥:自注意力结果需要经过softmax归一化,导致自注意力结果之间是互斥的,无法同时关注多个输入。使用多组自注意力模型产生多组不同的注意力结果,则不同组注意力模型可能关注到不同的输入,从而增强模型的表达能力。

5.4.3 在模型中的应用

在Transformer中，multi-head attention以三种不同的方式使用：

multi-head self attention：标准的多头自注意力层，用在encoder的第一个多头自注意力层。所有key，value和query来自同一个地方，即encoder中前一层的输出。在这种情况下，encoder中的每个位置都可以关注到encoder上一层的所有位置。
masked-self-attention：用在decoder中，序列的每个位置只允许看到当前位置之前的所有位置，这是为了保持解码器的自回归特性，防止看到未来位置的信息。
encoder-decoder attention：用于encoder block的第二个多头自注意力层。query来自前面的decoder层，而keys和values来自encoder的输出memory。这使得decoder中的每个位置都能关注到输入序列中的所有位置。

encoder-decoder attention层可以使解码器在每个时间步，把注意力集中到输入序列中感兴趣的位置。
。

以句子“hello world”翻译为“你好世界”为例，当解码器准备生成“你”这个字的时候，它的输入（query）会与输入序列中的所有单词（“hello"和"world”）进行比较。在这个特定的时间步骤里，如果解码器的输入query与“hello”的相似度最高，那么模型的注意力就会主要集中在“hello”上。这意味着，在生成“你”这个字时，模型认为“hello”是最相关的词，因此将更多的信息从“hello”传递到解码器，帮助它更准确地生成翻译。

5.5 FFN

Transformer论文逐段精读【论文精读】- 01:00:04

编码器和解码器中的每个层都包含一个全连接的前馈网络，该前馈网络分别且相同地应用于每个位置。该前馈网络包括两个线性变换，并在两个线性变换中间有一个ReLU激活函数。

$\text{FFN}(x) = \max(0, xW_1 + b_1) W_2 + b_2$

Position-wise的意思是，这个多层感知机（MLP）对序列中的每个token都独立地应用一次，且应用的是同一个MLP。这意味着MLP只作用于最后一个维度(d=512)。

因为前面的attention层已经捕获了输入序列的相关信息，并进行了一次汇聚（通过拼接后用(W)映射回(d)维）。所以attention层的结果已经包含了序列中我们感兴趣的信息，因此，在进行MLP映射到我们想要的语义空间时，只需对每个位置（token）单独进行MLP处理。

从attention层抽取序列信息到MLP映射到所需的语义空间的非线性变换，构成了transformer处理信息的基础过程。

尽管两层都是线性变换，但它们在层与层之间使用不同的参数。另一种描述方式是两个内核大小为1的卷积。输入和输出的维度都是 $d_{\text{model}} = 512$ ，内层维度是 $d_{ff} = 2048$ 。（也就是第一层输入512维，输出2048维；第二层输入2048维，输出512维）。

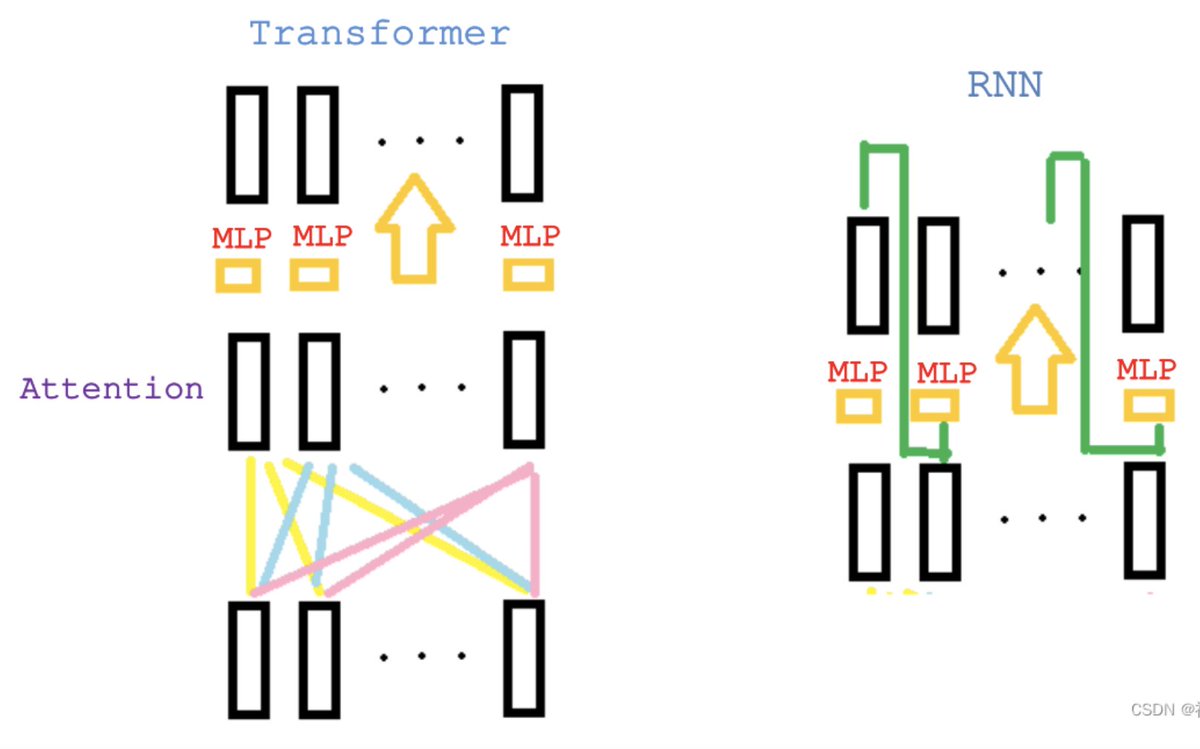
RNN是把上一时刻信息作为输入（和t时刻输入一起），传递给当前时刻，并用MLP做语义转换。
Transformer是通过attention层直接关联到全局的序列信息，然后用MLP做语义转换。

1	MLP的作用是对输入信息进行进一步的加工和抽象，以便捕捉到更深层次的语义关系和模式。

5.6 词嵌入和Softmax

我们使用学习到的嵌入将输入token和输出token转换为 $d_{\text{model}}$ 维的向量。我们还使用普通的线性变换和softmax函数将解码器输出转换为预测的下一个token的概率。在我们的模型中,输入输出两个嵌入层,和pre-softmax线性变换共享相同的权重矩阵(这样训练起来简单一些)。最后我们将这些权重乘以 $\sqrt{d_{\text{model}}}$ (比如512)。

这是因为一般会把一个向量的L2范数学到接近1,这样向量维度越大,学到的权重值就会很小。但是位置编码是不会这样学成L2范数接近1的。所以把权重乘上 $\sqrt{d_{\text{model}}}$ 之后,token嵌入和位置编码(Positional Encoding)才接近统一量级。(都在-1到1之间)

5.7 位置编码(Positional Encoding)

Attention计算时本身是不考虑位置信息的,这样序列顺序变化结果也是一样的。所以我们必须在序列中加入关于词符相对或者绝对位置的一些信息。为此,我们将“位置编码”添加到token嵌入中。二者维度相同(例如 $d_{\\text{model}} = 512$ ),所以可以相加。有多种位置编码可以选择,例如通过学习得到的位置编码和固定的位置编码。

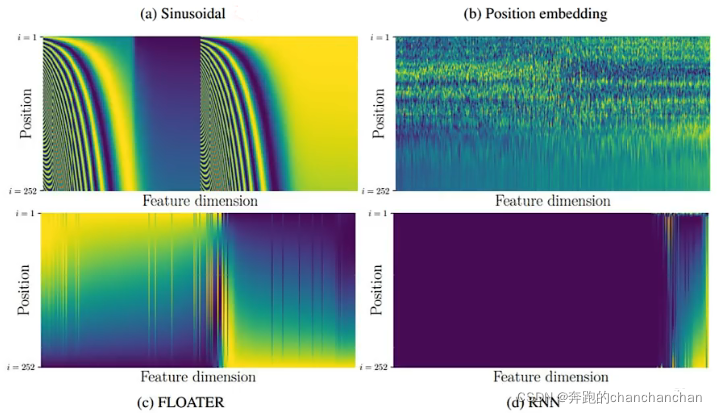
在这项工作中,我们使用不同频率的正弦和余弦函数:

$PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$

$PE_{(pos,2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$

其中 $pos$ 是位置, $i$ 是维度。也就是说,位置编码的每个维度对应于一个正弦曲线。这些波长形成一个从 $2\pi$ 到 $10000 \cdot 2\pi$ 的幂级数。我们选择这个函数是因为我们假设它会让模型很容易学习对相对位置的关注,因为对任意确定的偏移 $k$ , $PE_{pos+k}$ 可以表示为 $PE_{pos}$ 的线性函数。最终编码向量每个元素值都是在-1到1之间。

此外,我们会将编码器和解码器堆栈中的嵌入和位置编码的和再加一个dropout。对于基本模型,我们使用的dropout比例是 $P_{drop} = 0.1$ 。

5.8 为什么使用自注意力机制

在本节中，我们比较了self-attention与循环层和卷积层的各个方面，选择使用self-attention是为了解决三个主要问题：

每层计算的总复杂度：我们希望这个复杂度尽可能低。
顺序计算量：越少表示并行度越高。顺序计算量即下一步计算需要等待前面多少步骤完成。
网络中长距离依赖之间的路径长度：影响长距离依赖性能力的一个关键因素是前向和后向信号在网络中传播的路径长度。输入和输出序列中任意位置之间的路径越短，学习长距离依赖性就越容易。

我们还比较了由不同层类型组成的网络中任意两个输入和输出位置之间的最大路径长度。以下是关于attention的分析：

计算复杂度：矩阵(Q*K)的计算，其中两个矩阵都是(n)行(d)列，复杂度为 $O(n^2 \cdot d)$ ，其他计算量相对较小；
顺序计算量：矩阵内部并行度很高，整个计算主要是矩阵乘法，所以顺序计算量为(O(1))；
最大路径长度：从一个点关联到任何一个点的路径长度。Attention能一次性看到整个序列，所以只需要一次操作，复杂度为(O(1))。

在实际应用中，attention机制相比于RNN和CNN，对模型的假设更少，这意味着模型需要更多的数据和更大的模型尺寸才能达到类似的效果。因此，基于transformer的模型通常规模较大，训练成本较高。

attention的计算复杂度是如何得到的？：
Attention机制的计算复杂度主要来源于它的核心操作,即计算查询(Queries)和键(Keys)之间的点积,并应用softmax函数来得到权重,然后这些权重被用于加权和值(Values)。具体地,对于一个输入序列,我们考虑以下几个维度:

$n$ : 序列的长度,即输入中的token数量。
$d$ : 每个token的维度,即Queries、Keys和Values的维度。

在自注意力机制中,每个输入的token都会被转换成对应的Query、Key和Value。然后,对于序列中的每一个Query,都会与所有Keys进行点积操作来计算相似度分数,这个过程的复杂度是 $O(n^2 \cdot d)$ ,因为:

对于每个Query,都需要与 $n$ 个Key进行点积,每次点积操作的复杂度是 $O(d)$ 。
序列中有 $n$ 个这样的Queries。

因此,总的计算复杂度为所有Queries和所有Keys点积操作的总和,即 $O(n^2 \cdot d)$ 。

6.实验

6.1 训练数据和批处理

我们在标准的WMT 2014 English-German dataset上进行了训练,其中包含约450万个句子对。这些句子使用byte-pair编码(BPE)进行编码,源语句和目标语句共享大约37000个词符的词汇表。对于英语-法语翻译,我们使用更大的WMT 2014 English-French dataset,它包含3600万个句子,并将词符分成32000个word-piece词汇表。序列长度相近的句子一起进行批处理。每个训练批次的句子对包含大约25000个源词符和25000个目标词符。

BPE编码是因为英语/德语中有很多词根变化,如动词的不同形式等。BPE可以有效减小词表大小同时保留重要的语义信息。共用词表可以让编码器和解码器共享一个embedding,简化模型并共享权重。

6.2 硬件和时间

我们在一台配备了8个NVIDIA P100 GPU的机器上训练模型。使用本文描述的超参数的基础模型,每个训练步骤耗时约0.4秒。基础模型共训练了10万步或12小时。对于我们的大型模型(详见表3),每步耗时约1.0秒,共训练了30万步或3.5天。

后来,由于TPU非常适合进行大规模矩阵乘法,Google推荐使用TPU进行训练。

6.3 优化器

我们使用Adam优化器,其中 $\beta_1=0.9$ , $\beta_2=0.98$ 并且 $\epsilon=10^{-9}$ 。学习率按照以下公式动态调整:

$lrate = d_{\text{model}}^{-0.5} \cdot \min(step\_num^{-0.5}, step_num \cdot warmup\_steps^{-1.5})$

这意味着学习率在前 warmup_steps 步中线性增加,之后与步数的平方根成反比减小。我们设置 warmup_steps = 4000。

6.4 正则化

训练期间我们采用两种正则化策略:

Residual Dropout:我们在每个子层的输出上应用dropout,即在子层输出进入残差连接和LayerNorm之前。此外,在编码器和解码器的token embedding加上Positional Encoding时也使用了dropout。对于基础模型,我们使用的dropout概率为0.1。
Label Smoothing:训练过程中,我们使用了label smoothing,其值为 $\\epsilon_{ls} = 0.1$ 。这使模型变得不那么自信,虽然模型学到的信息更加不确定,但这提高了准确性和BLEU得分。

在没有使用Label Smoothing的情况下，如果我们有一个分类任务，真实的标签可能会被表示为一个one-hot向量。例如，在一个三分类任务中，第一个类的标签是[1, 0, 0]，这意味着模型被鼓励去预测绝对的置信度为100%属于第一类，0%属于其他类。这可能会导致模型过于自信，过拟合训练数据，对新的或略有差异的数据表现不佳。

使用Label Smoothing后，我们可能会将这个标签修改为如[0.9, 0.05, 0.05]。这样，即使模型最确信的预测是正确的，它也不能达到100%的置信度，这迫使模型学习到更加平滑的、不那么极端的概率分布，有助于提高模型对不见过的数据的泛化能力。

6.5 模型参数

7.评价

Transformer（attention机制）几乎能用在所有NLP任务上，类CNN对整个CV领域的革新（不需要那么多的特征提取或者模型建模，学会CNN就行了）。Transformer也是一样，不需要那么多的文本预处理，不需要为每个任务设计不同的架构。
而且现在transformer在CV、语音、video等领域也广泛使用，等于一个架构可以适用所有领域，任何一点突破在别的领域都能被使用，减少技术的应用时间。而且Transformer可以融合多模态的数据（文字、图片、语音等），大家都要同一个架构提取特征的话，可以都抽取到同一个语义空间，使得我们可以用文字、图片、语音等训练更大更好的模型。

虽然Transformer效果这么好，但是对它的理解还在初级阶段。

最新的一些结果表明，attention在里面只是起到一个聚合序列信息的作用 ，但是后面的MLP/残差连接是缺一不可的，如果去掉的话，模型是基本训练不出什么的

Attention不会对序列的顺序建模，为何能打败RNN？RNN可以显式地建模序列信息，不是应该比attention更好。现在大家觉得attention使用了更广泛的归纳偏置，使得他能处理更一般化的信息；这也是attention没有做空间上的假设吗，但是比CNN/RNN能做到更好的效果。代价就是假设更一般，所以抓取数据信息能力变差，必须使用更大的模型和更多的数据才能训练到一个比较好的效果。

一.Introduction

在过去的使用场景中，模型的输入通常只有一个单独的向量，而模型的输出则是预测的数值或类别,见下图：

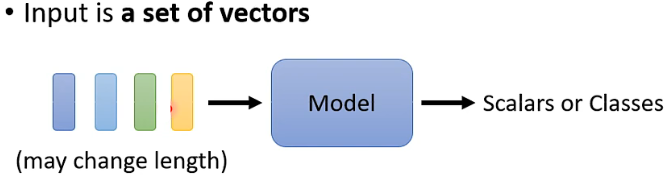
但是假设输入的是一排向量（或序列），且向量的长度不是固定的，例如声音信号、语句、基因序列等，如下图：

而对于模型输出而言，可以分为如下图所示的三种类型，即输入输出序列长度不变，只有一个输出和输出长度不确定：

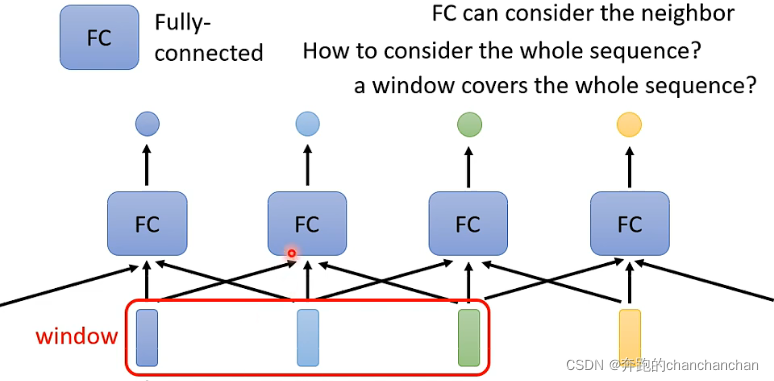
以第一种类型为例，常规的想法是采取各个击破的方法，给每个向量添加一个全连接层，从而得到我们想要的输出，但是这样的方法并没有考虑到各个输入向量之间的关系:

因此为了让全连接层能够考虑到上下文信息之间的关系，可以将多个相邻的输入向量或序列串联起来给到全连接层，但是到底需要多少个相邻的输入向量，以及如何能够把整个序列作为输入，这就是Self-attention所要做的工作。

二.Self-attention

Self-attention的内部机制大致如上图所示，每个输出 $b^i$ 都考虑了所有的输入 $a^j$ 。以单个输出 $b^1$ 为例，Self-attention的具体操作流程如下：

---------- Self-attention流程·BEGIN ----------

$\alpha$ : 两个输入向量之间的关联性
$\alpha^{'}$ : 经过softmax后，两个输入向量之间的关联性
a：输入
b：输出
W：权重

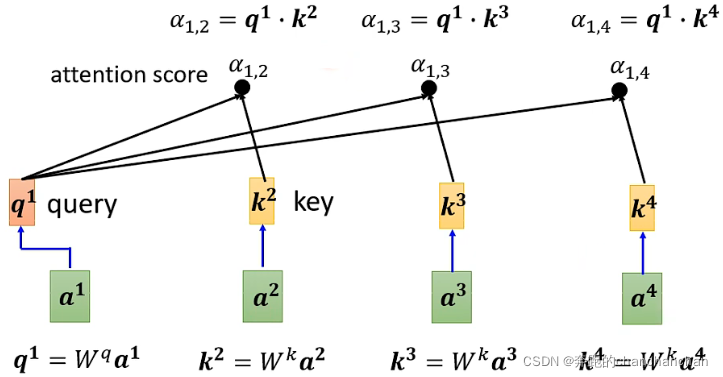
Step1: 将两个输入向量各自乘以 $W^q和W^k$ ,得到q和k，再将q和k做点乘，从而得到两个输入向量之间的关联性，记作 $\alpha$ :

如下图所示，分别得到输入向量 $a^1$ $a^2$ 之间的关联性 $\alpha_{1,2}$ ,输入向量 $a^1$ 和 $a^3$ 之间的关联性 $\alpha_{1,3}$ ,输入向量 $a^1$ 和 $a^4$ 之间的关联性 $\alpha_{1,4}$ :

Step2: 通常情况下，还需要考虑输入向量和自身的关联性，然后将计算得到的所有关联性 $\alpha$ 扔给softmax函数，得到 $\alpha^{'}$ :

Step3: 根据输入向量之间的关联性 $\alpha^{'}$ 进一步提取向量中的重要信息，即将每个输入向量 $a^i$ 乘以 $W^v$ 得到 $v^i$ ,并与其相关的关联性分数 $\alpha^{'}_{1,i}$ 相乘，最后将结果累加得到 $b^1$ :

这样一来，假设输入向量 $a^1和a^2$ 的关联性比较大，即 $\alpha^{'}_{1,2}$ 的值较大，根据累加得到的 $b^1$ 也会更接近 $\alpha_{1,2}^{'}$

---------- Self-attention流程·END ----------

实际上，Self-attention的输出 $b^1、b^2、b^3、b^4$ 可以同时得到。从矩阵运算的角度来说，Self-attention的具体操作流程如下:

---------- Self-attention流程·矩阵角度·BEGIN ----------

Step1: 将输入向量 $a^1、a^2、a^3、a^4$ 按列组合成一个矩阵I，与 $W^q$ 相乘得到矩阵Q，其中矩阵Q包含了所有输入向量对应的query，同理可以得到key和value对应的矩阵K和V：

Step2: 将各个向量对应的key按行组合，与输入向量 $a^1$ 相乘，得到与输入向量 $a^1$ 之间的所有关联性分数 $\alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4}$ :

由此可知，将矩阵K转置后，与矩阵Q相乘得到矩阵A，其中矩阵A包含了所有输入向量之间的关联性分数:

然后再将矩阵A给到Softmax激活函数，得到矩阵 $A^{'}$ :

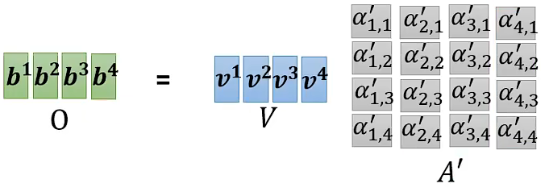
Step3: 最后将各个输入向量对应的value按列组合成一个矩阵V，并与矩阵 $A^{'}$ :

---------- Self-attention流程·矩阵角度·END ----------

三.Multi-head Self-attention

Multi-head Self-attention就是由多个单独的Self-attention堆叠而成，每个Self-attention之间具有独立的参数矩阵，相互之间不共享参数。

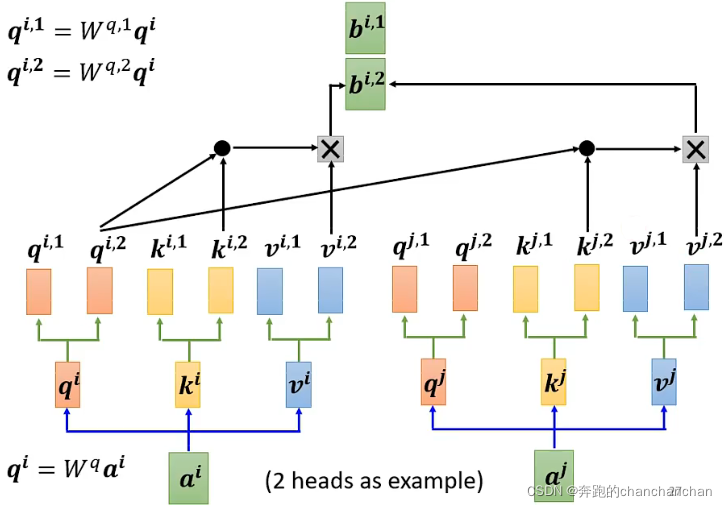
以2 heads为例，首先通过输入向量 $a^i$ 与矩阵 $W^q$ 相乘得到 $q^i$ ，再将向量 $q^i$ 与2个不同的矩阵相乘得到两个参数 $q^{i,1}$ 和 $q^{i,2}$

同理可以得到参数 $k^{i,1}、k^{i,2}、v^{i,1}和v^{i,2}$ 。对于另一个输入向量 $a^j$ ，同样可以得到两组参数 $q^{j,1}和q^{j,2}，k^{j,1}和k^{j,2}，v^{j,1}和v^{j,2}$ 。
在计算关联度分数时，只需先对第一类的参数进行计算，得到 $b^{i,1}$

再对第二类的参数进行计算，得到 $b^{i,2}$ ，如下图所示:

最后将 $b^{i,1}$ 和 $b^{i,2}$ 拼接起来，与矩阵 $W^O$ 相乘得到Multi-head Self-attention的第i个输出 $b^i$ :

四.Position Encoding

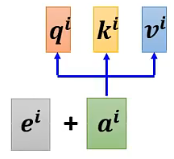
由于在Self-attention的计算中不包含位置信息，因此为了加入位置信息，需要在每个位置都定义一个位置向量 $e^i$ ，并且直接加到输入向量 $a^i$ 上

位置向量 $e^i$ 通常是手动设置，也可以通过学习得到:

五.Transformer

Transformer本质上是一个Sequence-to-sequence(Seq2seq) 的模型，它的输出序列长度不再是固定的，而是由模型自身决定：

Sequence-to-sequence(Seq2seq)的模型结构通常如上图所示，由Encoder对输入向量（或序列）进行处理，处理完之后给到Decoder，并由Decoder决定输出向量（或序列）

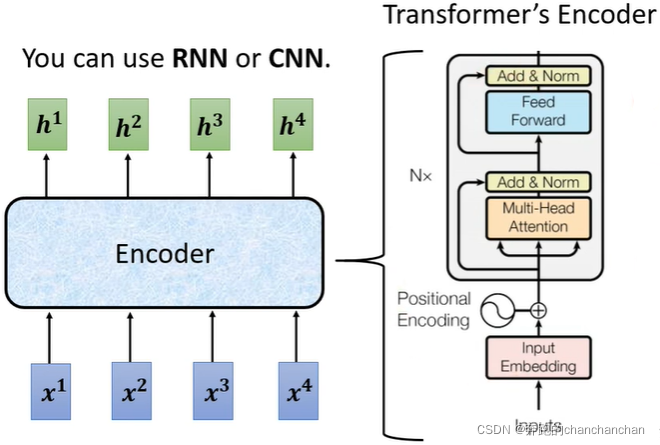
5.1 Encoder

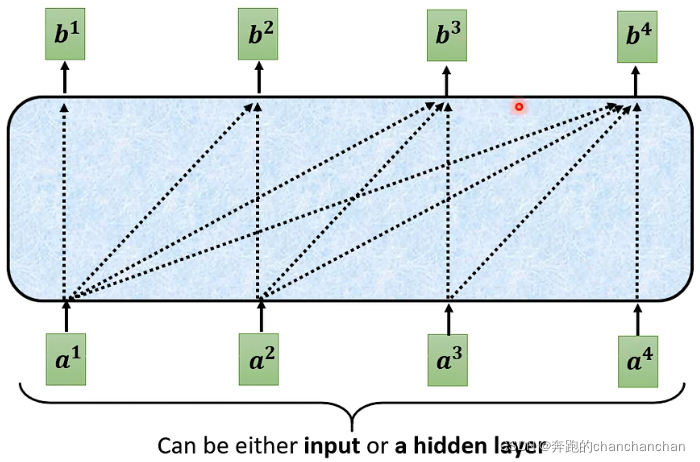
其中Encoder部分的作用是给定一组向量（或序列），输出一组相同长度的向量（或序列）:

根据原论文Attention Is All You Need中的介绍，进一步拆解它的内部结构可以看到，输入向量b经过Self-attention得到向量a，同时由相应的输入向量b通过跳跃连接与向量a相加，经过一次Layer Norm操作后得到向量c。将向量c给到全连接层得到向量d，并与自身通过跳跃连接相加得到向量e，最后再做一次Layer Norm操作得到向量f:

5.2 Decoder

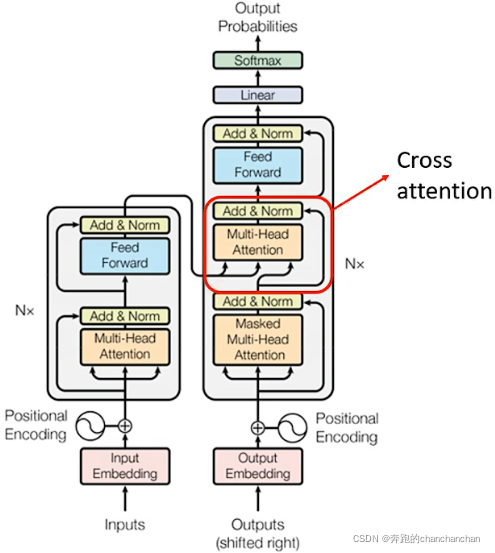
根据Attention Is All You Need中的介绍，Decoder的内部结构可以看到:

在Decoder中，Encoder的输出在经过cross attention处理之后，来作为Decoder的输入，另外还需要给予一个one-hot形式的BEGIN信号让Decoder开始输出一个向量。

在NLP任务中，这个向量的长度由任务所需要的语言单词或短语的数量来决定，例如识别的语言是中文，那么这个向量可能就需要包含所有的中文汉字或常见字。同时为了让模型自己决定需要输出多长的序列，向量中还包含了一个END信号。向量中的每个单词或短语都带有对应的模型预测概率，概率最高的那一项才是最终的输出

接下来再将第一个输出给到Decoder，作为新的输入，从而得到第二个输出。以此为例，新的输出再次给到Decoder中，直到输出END信号表示向量输出的结束。

正是因为新的输入是由之前的输出所得到的，因此在Decoder中使用了Masked Multi-Head Attention，与Encoder中的Multi-Head Attention所不同的是，在计算输出的时候只考虑自身及其左边的输入向量，而不需要考虑右边那些还没得到的输入向量，如下图：

5.3 Cross Attention

Decoder部分不仅有自身的输入向量，还有Encoder部分的输出作为输入向量。而Encoder部分的输出与Decoder中Masked Multi-Head Attention的输出一起被送到Multi-Head Attetion进行处理，这部分就叫Cross Attention，如上图:

Cross Attention的具体实现流程如下：

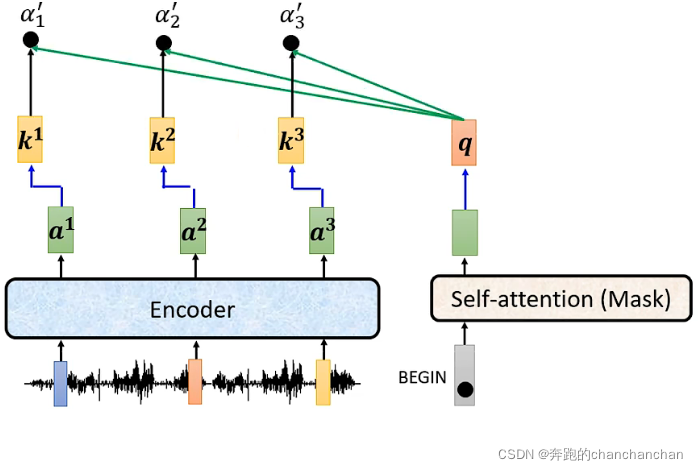
---------- Cross Attention流程·BEGIN ----------

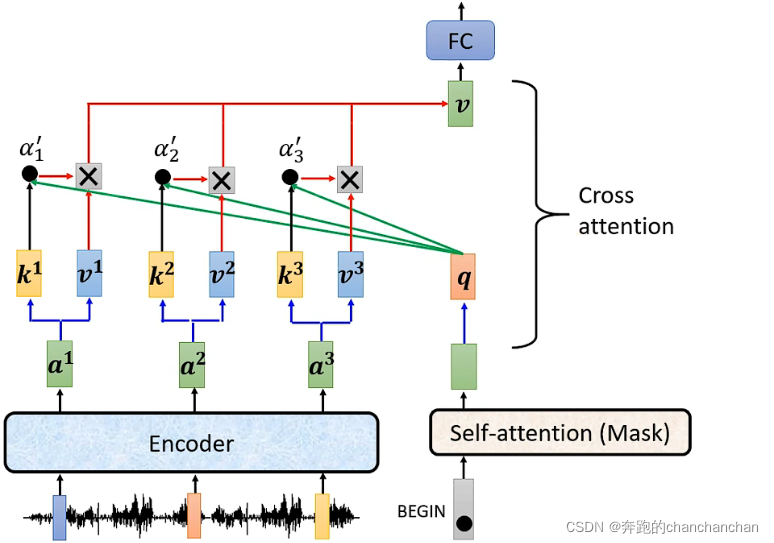
1.Encoder的输出分别与各自对应的矩阵 $W^k$ 相乘得到key值，Decoder中Masked Multi-Head Attention的输出与矩阵 $W^q$ 相乘得到query值，然后两者做点乘得到关联性分数 $\alpha$ :

2.Encoder的输出分别与各自对应的矩阵 $W^v$ 相乘得到value值，然后与关联性分数 $\alpha$ 相乘，并将所有的结果累加起来。累加后的结果再给到全连接层，得到最终的输出:

---------- Cross Attention流程·END ----------