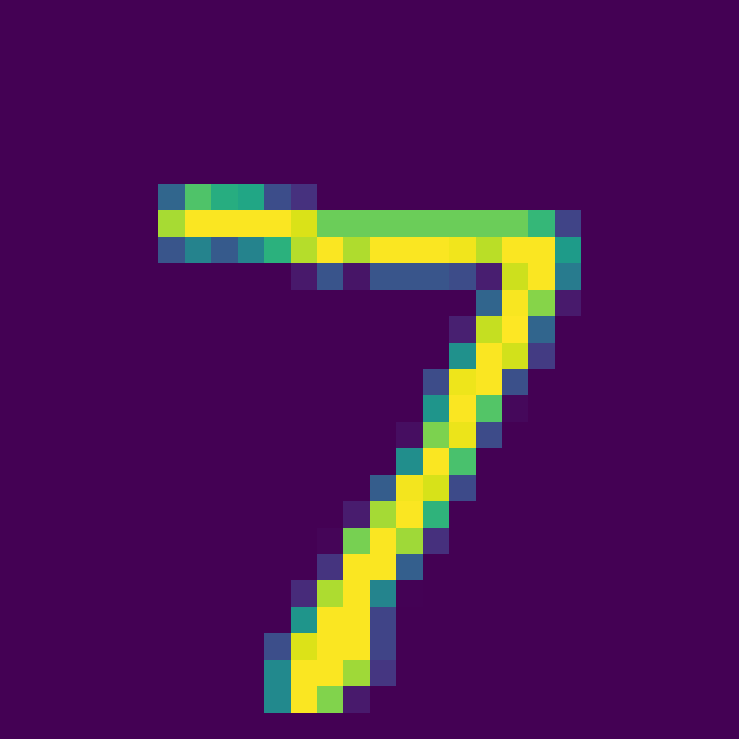使用单层全连接SNN识别MNIST

本节教程将介绍如何使用编码器与替代梯度方法训练一个最简单的MNIST分类网络。

1.从头搭建一个简单的SNN网络

在PyTorch中搭建神经网络时，我们可以简单地使用nn.Sequential将多个网络层堆叠得到一个前馈网络，输入数据将依序流经各个网络层得到输出。

MNIST数据集包含若干尺寸为28x28的8位灰度图像，总共有0~9共10个类别。以MNIST的分类为例，一个简单的单层ANN网络如下：


nn.Sequential(
    nn.Flatten(),
    nn.Linear(28 * 28, 10, bias=False),
    nn.Softmax()
    )

我们也可以用完全类似结构的SNN来进行分类任务。

就这个网络而言，我们只需要

1.去掉所有的激活函数
2.神经元添加到原来激活函数的位置

这里我们选择的是LIF神经元。

神经元之间的连接层需要用spikingjelly.activation_based.layer包装：


nn.Sequential(
    layer.Flatten(),
    layer.Linear(28 * 28, 10, bias=False),
    neuron.LIFNode(tau=tau, surrogate_function=surrogate.ATan())
    )

其中膜电位衰减常数 $\tau$ 需要通过参数 $\tau$ 设置，替代函数这里选择surrogate.ATan。

2.训练SNN网络

首先指定好训练参数如学习率等以及若干其他配置

优化器默认使用Adam，以及使用泊松编码器，在每次输入图片时进行脉冲编码


# 使用Adam优化器
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
# 使用泊松编码器
encoder = encoding.PoissonEncoder()

训练代码的编写需要遵循以下三个要点：

1. 脉冲神经元的输出是二值的，而直接将单次运行的结果用于分类极易受到编码带来的噪声干扰。因此一般认为脉冲网络的输出是输出层一段时间内的\ 发放频率\ （或称发放率），发放率的高低表示该类别的响应大小。因此网络需要运行一段时间，即使用\ T\ 个时刻后的\ 平均发放率\ 作为分类依据。
1. 我们希望的理想结果是除了正确的神经元\ 以最高频率发放\ ，其他神经元\ 保持静默\ 。常常采用交叉熵损失或者MSE损失，这里我们使用实际效果更好的MSE损失。
1. 每次网络仿真结束后，需要\ 重置\ 网络状态

结合以上三点，得到训练循环的核心代码如下：


for epoch in range(start_epoch, args.epochs): #训练循环
    start_time = time.time()
    net.train()
    train_loss = 0
    train_acc = 0
    train_samples = 0
    for img, label in train_data_loader:
        optimizer.zero_grad()
        img = img.to(args.device)
        label = label.to(args.device)
        label_onehot = F.one_hot(label, 10).float()

        # 混合精度训练
        if scaler is not None: #
            with amp.autocast():#自动转换类型
                out_fr = 0.
                # 运行T个时间步
                for t in range(args.T):
                    encoded_img = encoder(img)
                    out_fr += net(encoded_img)
                out_fr = out_fr / args.T
                # out_fr是shape=[batch_size, 10]的tensor
                # 记录整个仿真时长内，输出层的10个神经元的脉冲发放率
                loss = F.mse_loss(out_fr, label_onehot)
                # 损失函数为输出层神经元的脉冲发放频率，与真实类别的MSE
                # 这样的损失函数会使得：当标签i给定时，输出层中第i个神经元的脉冲发放频率趋近1，而其他神经元的脉冲发放频率趋近0
            scaler.scale(loss).backward() #反向传播
            scaler.step(optimizer) #更新参数
            scaler.update()
        else:
            out_fr = 0.
            for t in range(args.T):
                encoded_img = encoder(img)
                out_fr += net(encoded_img)
            out_fr = out_fr / args.T
            loss = F.mse_loss(out_fr, label_onehot)
            loss.backward()
            optimizer.step()

        train_samples += label.numel()
        train_loss += loss.item() * label.numel()
        # 正确率的计算方法如下。认为输出层中脉冲发放频率最大的神经元的下标i是分类结果
        train_acc += (out_fr.argmax(1) == label).float().sum().item()
        
        # 优化一次参数后，需要重置网络的状态，因为SNN的神经元是有“记忆”的
        functional.reset_net(net)

完整的代码位于activation_based.examples.lif_fc_mnist.py，在代码中我们还使用了Tensorboard来保存训练日志。可以直接在命令行运行它：


$ python -m spikingjelly.activation_based.examples.lif_fc_mnist --help
usage: lif_fc_mnist.py [-h] [-T T] [-device DEVICE] [-b B] [-epochs N] [-j N]
                    [-data-dir DATA_DIR] [-out-dir OUT_DIR]
                    [-resume RESUME] [-amp] [-opt {sgd,adam}]
                    [-momentum MOMENTUM] [-lr LR] [-tau TAU]

LIF MNIST Training

optional arguments:
-h, --help          show this help message and exit
-T T                simulating time-steps
-device DEVICE      device
-b B                batch size
-epochs N           number of total epochs to run
-j N                number of data loading workers (default: 4)
-data-dir DATA_DIR  root dir of MNIST dataset
-out-dir OUT_DIR    root dir for saving logs and checkpoint
-resume RESUME      resume from the checkpoint path
-amp                automatic mixed precision training
-opt {sgd,adam}     use which optimizer. SGD or Adam
-momentum MOMENTUM  momentum for SGD
-lr LR              learning rate
-tau TAU            parameter tau of LIF neuron

需要注意的是，训练这样的SNN，所需显存数量与仿真时长 T 线性相关，更长的 T 相当于使用更小的仿真步长，训练更为“精细”，但训练效果不一定更好。 T
太大时，SNN在时间上展开后会变成一个非常深的网络，这将导致BPTT计算梯度时容易衰减或爆炸。

另外由于我们使用了泊松编码器，因此需要较大的 T保证编码带来的噪声不太大。

3.训练结果

取tau=2.0,T=100,batch_size=64,lr=1e-3，对应的运行命令为

1
2
3


python -m spikingjelly.activation_based.examples.lif_fc_mnist -tau 2.0 -T 100 -device cuda:0 -b 64 -epochs 100 -data-dir <PATH to MNIST> -amp -opt adam -lr 1e-3 -j 8

其中为了加快训练速度，启用了混合精度训练。训练100个Epoch后，将会输出两个npy文件以及训练日志。测试集上的最高正确率为92.9%，通过matplotlib可视化得到的正确率曲线如下：

选取测试集中第一张图片：

用训好的模型进行分类，得到分类结果

1
2
3


Firing rate: [[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]]

通过visualizing模块中的函数可视化得到输出层的电压以及脉冲如下图所示：

可以看到除了正确类别对应的神经元外，其它神经元均未发放任何脉冲。完整的训练代码可见 activation_based/examples/lif_fc_mnist.py 。