internshipSNN

神经元

本教程作者： fangwei123456

本节教程主要关注 :class:spikingjelly.activation_based.neuron，介绍脉冲神经元。


1.脉冲神经元模型

在 spikingjelly 中，我们约定，只能输出脉冲，即0或1的神经元，都可以称之为“脉冲神经元”。使用脉冲神经元的网络，进而也可以称之为脉冲神经元网络(Spiking Neural Networks, SNNs)。
class:spikingjelly.activation_based.neuron 中定义了各种常见的脉冲神经元模型，我们以 :class:spikingjelly.activation_based.neuron.IFNode 为例来介绍脉冲神经元。

首先导入相关的模块：

1
2
3
4
import torch
from spikingjelly.activation_based import neuron
from spikingjelly import visualizing
from matplotlib import pyplot as plt

1.1 IF神经元层的参数

新建一个IF神经元层：

1
if_layer = neuron.IFNode()

IF神经元层有一些构造参数，在API文档中对这些参数有详细的解释，我们暂时只关注下面几个重要的参数：

  • v_threshold： 神经元的阈值电压

  • v_reset： 神经元的重置电压。如果不为 None，当神经元释放脉冲后，电压会被重置为 v_reset；如果设置为 None，则电压会被减去 v_threshold

  • surrogate_function： 反向传播时用来计算脉冲函数梯度的替代函数

你可能会好奇这一层神经元的数量是多少。对于 :class:spikingjelly.activation_based.neuron.IFNode 中的绝大多数神经元层，神经元的数量是在初始化或调用 reset() 函数重新初始化后，根据第一次接收的输入的 shape 自动决定的。


1.2 脉冲神经元的状态和记忆

与RNN中的神经元非常类似，脉冲神经元也是有状态的，或者说是有记忆。脉冲神经元的状态变量，一般是它的膜电位 V[t]。因此，:class:spikingjelly.activation_based.neuron 中的神经元，都有成员变量 v。可以打印出刚才新建的IF神经元层的膜电位：

1
2
print(if_layer.v)
# if_layer.v=0.0

可以发现，现在的 if_layer.v 是 0.0，因为我们还没有给与它任何输入。我们给与几个不同的输入，观察神经元的电压的 shape，可以发现它与输入的
数量是一致的：

1
2
3
4
5
6
7
8
9
10
11
12

x = torch.rand(size=[2, 3])
if_layer(x)
print(f'x.shape={x.shape}, if_layer.v.shape={if_layer.v.shape}')
# x.shape=torch.Size([2, 3]), if_layer.v.shape=torch.Size([2, 3])
if_layer.reset()

x = torch.rand(size=[4, 5, 6])
if_layer(x)
print(f'x.shape={x.shape}, if_layer.v.shape={if_layer.v.shape}')
# x.shape=torch.Size([4, 5, 6]), if_layer.v.shape=torch.Size([4, 5, 6])
if_layer.reset()

1.3 脉冲神经元的动态方程

脉冲神经元是有状态的，在输入下一个样本前，一定要先调用 reset() 函数清除之前的状态。

V[t] 和输入X[t] 的关系是什么样的？在脉冲神经元中，V[t] 不仅取决于当前时刻的输入 X[t]，还取决于它在上一个时刻末的膜电位 V[t-1]。

通常使用阈下（指的是膜电位不超过阈值电压 VthresholdV_{threshold} 时）神经动态方程 dV(t)dt=f(V(t),X(t))\frac{\mathrm{d}V(t)}{\mathrm{d}t} = f(V(t), X(t)) 描述连续时间的脉冲神经元的充电过程，例如对于IF神经元，充电方程为：

dV(t)dt=V(t)+X(t) \frac{\mathrm{d}V(t)}{\mathrm{d}t} = V(t) + X(t)

:class:spikingjelly.activation_based.neuron 中的神经元，使用离散的差分方程来近似连续的微分方程。在差分方程的视角下，IF神经元的充电方程为：

V[t]−V[t−1]=X[t] V[t] - V[t-1] = X[t]

因此可以得到V[t] 的表达式为

V[t]=f(V[t−1],X[t])=V[t−1]+X[t] V[t] = f(V[t-1], X[t]) = V[t-1] + X[t]

可以在 :class:spikingjelly.activation_based.neuron.IFNode.neuronal_charge 中找到如下所示的代码：

1
2
3

def neuronal_charge(self, x: torch.Tensor):
    self.v = self.v + x

1.4 神经元放电和重置过程

不同的神经元，充电方程不尽相同。但膜电位超过阈值电压后，释放脉冲，以及释放脉冲后，膜电位的重置都是相同的。因此它们全部继承自 :class:spikingjelly.activation_based.neuron.BaseNode，共享相同的放电、重置方程。可以在 :class:spikingjelly.activation_based.neuron.BaseNode.neuronal_fire 中找到释放脉冲的代码：

1
2
3

def neuronal_fire(self):
    self.spike = self.surrogate_function(self.v - self.v_threshold)

surrogate_function() 在前向传播时是阶跃函数，只要输入大于或等于0，就会返回1，否则会返回0。我们将这种元素仅为0或1的 tensor 视为脉冲。

释放脉冲消耗了神经元之前积累的电荷，因此膜电位会有一个瞬间的降低，即膜电位的重置。在SNN中，对膜电位重置的实现，有2种方式：

  • Hard方式：释放脉冲后，膜电位直接被设置成重置电压：

V[t]=VresetV[t] = V_{reset}

  • Soft方式：释放脉冲后，膜电位减去阈值电压：

V[t]=V[t]−VthresholdV[t] = V[t] - V_{threshold}

可以发现，对于使用Soft方式的神经元，并不需要重置电压VresetV_{reset} 这个变量。:class:spikingjelly.activation_based.neuron 中的神经元，在构造函数的参数之一 v_reset，默认为 1.0 ，表示神经元使用Hard方式；若设置为 None，则会使用Soft方式。在 :class:spikingjelly.activation_based.neuron.BaseNode.neuronal_fire.neuronal_reset 中可以找到膜电位重置的代码：

1
2
3
4
5
6
7
8

# The following codes are for tutorials. The actual codes are different, but have the similar behavior.

def neuronal_reset(self):
    if self.v_reset is None:
        self.v = self.v - self.spike * self.v_threshold
    else:
        self.v = (1. - self.spike) * self.v + self.spike * self.v_reset

2.描述离散脉冲神经元的三个方程

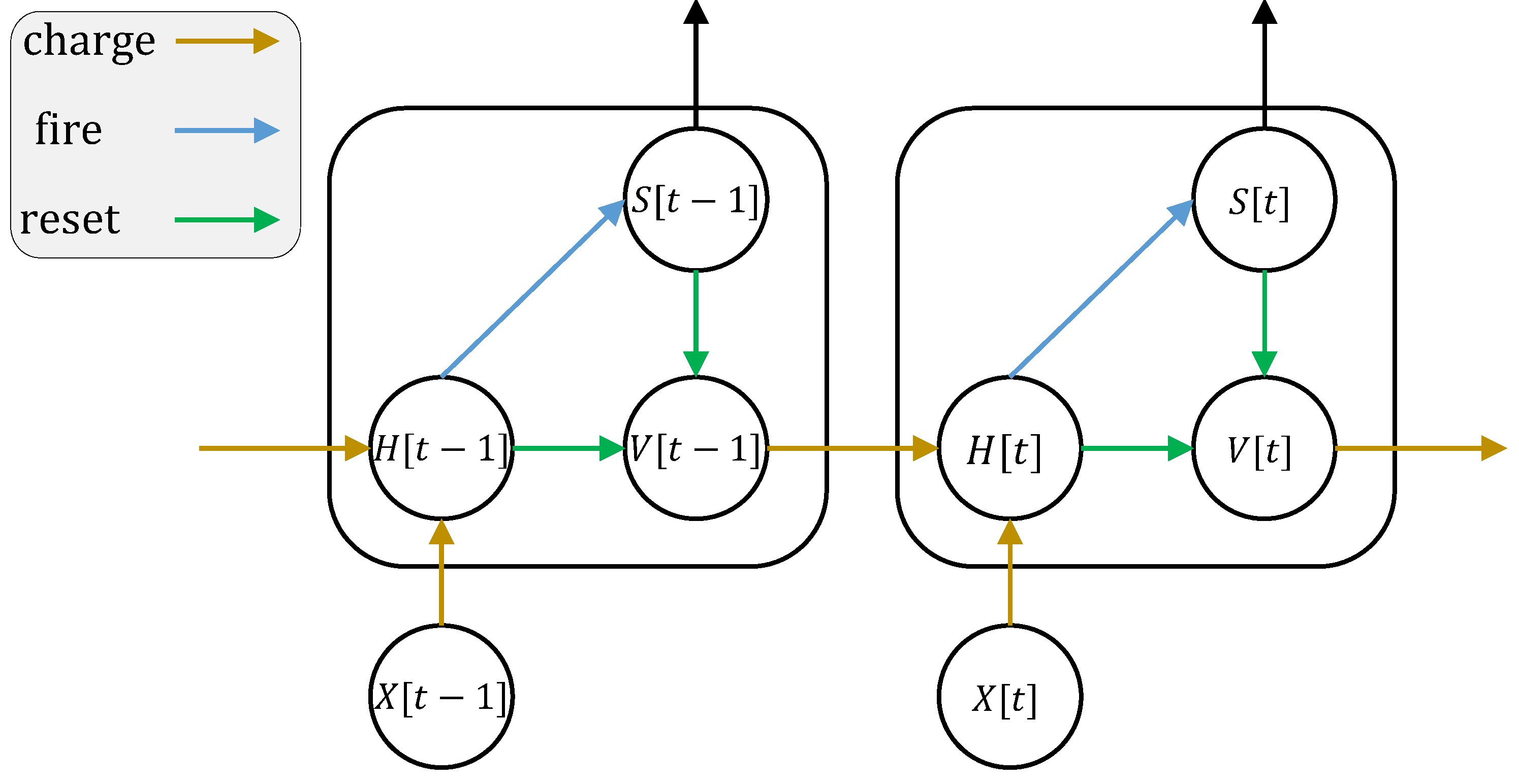
至此，我们可以用充电、放电、重置，这3个离散方程来描述任意的离散脉冲神经元。充电、放电方程为：

H[t]=f(V[t−1],X[t])S[t]=Θ(H[t]−Vthreshold) H[t] = f(V[t-1], X[t]) \\ S[t] = \Theta(H[t] - V_{threshold})

其中 Θ(x)\Theta(x) 即为构造函数参数中的 surrogate_function，是一个阶跃函数：

Θ(x)={1,x≥00,x<0 \Theta(x) = \begin{cases} 1, & x \geq 0 \\ 0, & x < 0 \end{cases}


Hard方式重置方程为：

V[t]=H[t]⋅(1−S[t])+Vreset⋅S[t] V[t] = H[t] \cdot (1 - S[t]) + V_{reset} \cdot S[t]

Soft方式重置方程为：

V[t]=H[t]−Vthreshold⋅S[t] V[t] = H[t] - V_{threshold} \cdot S[t]

其中X[t] 是外源输入，例如电压增量；为了避免混淆，我们使用H[t] 表示神经元充电后、释放脉冲前的膜电位；V[t] 是神经元释放脉冲后的膜电位；f(V[t-1], X[t]) 是神经元的状态更新方程，不同的神经元，区别就在于更新方程不同。

神经元的动态如下图所示：


3.仿真

接下来，我们将逐步给与神经元输入，并查看它的膜电位和输出脉冲。

现在让我们给与IF神经元层持续的输入，并画出其放电后的膜电位和输出脉冲：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
if_layer.reset()
x = torch.as_tensor([0.02])
T = 150
s_list = []
v_list = []
for t in range(T):
    s_list.append(if_layer(x))
    v_list.append(if_layer.v)

dpi = 300
figsize = (12, 8)
visualizing.plot_one_neuron_v_s(torch.cat(v_list).numpy(), torch.cat(s_list).numpy(), v_threshold=if_layer.v_threshold,
                                v_reset=if_layer.v_reset,
                                figsize=figsize, dpi=dpi)
plt.show()

我们给与的输入 shape=[1]，因此这个IF神经元层只有1个神经元。它的膜电位和输出脉冲随着时间变化情况如下：

下面我们将神经元层重置，并给与 shape=[32] 的输入，查看这32个神经元的膜电位和输出脉冲：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

if_layer.reset()
T = 50
x = torch.rand([32]) / 8.
s_list = []
v_list = []
for t in range(T):
    s_list.append(if_layer(x).unsqueeze(0))
    v_list.append(if_layer.v.unsqueeze(0))

s_list = torch.cat(s_list)
v_list = torch.cat(v_list)

figsize = (12, 8)
dpi = 200
visualizing.plot_2d_heatmap(array=v_list.numpy(), title='membrane potentials', xlabel='simulating step',
                            ylabel='neuron index', int_x_ticks=True, x_max=T, figsize=figsize, dpi=dpi)


visualizing.plot_1d_spikes(spikes=s_list.numpy(), title='membrane sotentials', xlabel='simulating step',
                        ylabel='neuron index', figsize=figsize, dpi=dpi)

plt.show()

结果如下：

4.步进模式和后端

在 :doc:../activation_based/basic_concept 中我们已经介绍过单步和多步模式，在本教程前面的内容中，我们使用的都是
单步模式。切换成多步模式非常简单，只需要设置 step_mode 即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

import torch
from spikingjelly.activation_based import neuron, functional
if_layer = neuron.IFNode(step_mode='s')
T = 8
N = 2
x_seq = torch.rand([T, N])
y_seq = functional.multi_step_forward(x_seq, if_layer)
if_layer.reset()

if_layer.step_mode = 'm'
y_seq = if_layer(x_seq)
if_layer.reset()


此外，部分神经元在多步模式下支持 cupy 后端。在 cupy 模式下，前反向传播会使用CuPy进行加速：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import torch
from spikingjelly.activation_based import neuron
if_layer = neuron.IFNode()
print(f'if_layer.backend={if_layer.backend}')
# if_layer.backend=torch

print(f'step_mode={if_layer.step_mode}, supported_backends={if_layer.supported_backends}')
# step_mode=s, supported_backends=('torch',)


if_layer.step_mode = 'm'
print(f'step_mode={if_layer.step_mode}, supported_backends={if_layer.supported_backends}')
# step_mode=m, supported_backends=('torch', 'cupy')

device = 'cuda:0'
if_layer.to(device)
if_layer.backend = 'cupy'  # switch to the cupy backend
print(f'if_layer.backend={if_layer.backend}')
# if_layer.backend=cupy

x_seq = torch.rand([8, 4], device=device)
y_seq = if_layer(x_seq)
if_layer.reset()


5.自定义神经元

如前所述，SpikingJelly使用充电、放电、重置三个方程来描述脉冲神经元，在 :class:BaseNode <spikingjelly.activation_based.neuron.BaseNode>
中可以找到对应的代码，单步模式下的前向传播 single_step_forward 函数即是由这3个过程组成：

1
2
3
4
5
6
7
8

# spikingjelly.activation_based.neuron.BaseNode
def single_step_forward(self, x: torch.Tensor):
    self.neuronal_charge(x)
    spike = self.neuronal_fire()
    self.neuronal_reset(spike)
    return spike

其中 neuronal_fire 和 neuronal_reset 对绝大多数神经元都是相同的，因而在 BaseNode 中就已经定义了。

不同的神经元主要是构造函数和充电方程 neuronal_charge 不同。因此，若想实现新的神经元，则只需要更改构造函数和充电方程即可。


------------------ 平方IF神经元·BEGIN ------------------

假设我们构造一种平方积分发放神经元，其充电方程为：

V[t]=f(V[t−1],X[t])=V[t−1]+X[t]2 V[t] = f(V[t-1], X[t]) = V[t-1] + X[t]^{2}

实现方式如下：

1
2
3
4
5
6
7

import torch
from spikingjelly.activation_based import neuron

class SquareIFNode(neuron.BaseNode):
    def neuronal_charge(self, x: torch.Tensor):
        self.v = self.v + x ** 2

:class:BaseNode <spikingjelly.activation_based.neuron.BaseNode> 继承自 :class:MemoryModule <spikingjelly.activation_based.base.MemoryModule>。

:class:MemoryModule <spikingjelly.activation_based.base.MemoryModule>默认的多步传播，是使用 for t in range(T) 来循环调用单步传播实现的。因此我们定义 neuronal_charge 后， single_step_forward 就已经是完整的了，进而 multi_step_forward 也可以被使用。


使用平方积分发放神经元进行单步或多步传播：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import torch
from spikingjelly.activation_based import neuron

class SquareIFNode(neuron.BaseNode):

    def neuronal_charge(self, x: torch.Tensor):
        self.v = self.v + x ** 2

sif_layer = SquareIFNode()

T = 4
N = 1
x_seq = torch.rand([T, N])
print(f'x_seq={x_seq}')

for t in range(T):
    yt = sif_layer(x_seq[t])
    print(f'sif_layer.v[{t}]={sif_layer.v}')

sif_layer.reset()
sif_layer.step_mode = 'm'
y_seq = sif_layer(x_seq)
print(f'y_seq={y_seq}')
sif_layer.reset()


输出为:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

x_seq=tensor([[0.7452],
        [0.8062],
        [0.6730],
        [0.0942]])
sif_layer.v[0]=tensor([0.5554])
sif_layer.v[1]=tensor([0.])
sif_layer.v[2]=tensor([0.4529])
sif_layer.v[3]=tensor([0.4618])
y_seq=tensor([[0.],
        [1.],
        [0.],
        [0.]])

------------------ 平方IF神经元·END ------------------