基本概念
1. 激活值的表示方法
spikingjelly.activation_based 使用取值仅为0或1的张量表示脉冲,例如:
1 | import torch |
输出结果:
1 | v = tensor([0.8156, 0.7492, 0.0531, 0.7591, 0.4431, 0.7992, 0.8907, 0.2421]) |
2. 数据格式
在 spikingjelly.activation_based 中,数据有两种格式,分别为:
-
表示单个时刻的数据,其
shape = [N, *],其中N是batch维度,*表示任意额外的维度 -
表示多个时刻的数据,其
shape = [T, N, *],其中T是数据的时间维度,N是batch维度,*表示任意额外的维度
3. 步进模式
spikingjelly.activation_based 中的模块,具有两种传播模式,分别是
- 单步模式(single-step):数据使用
shape = [N, *]的格式 - 多步模式(multi-step):数据使用
shape = [T, N, *]的格式
模块在初始化时可以指定其使用的步进模式 step_mode,也可以在构建后直接进行修改:
1 | import torch |
如果我们想给单步模式的模块输入 shape = [T, N, *] 的序列数据,通常需要手动做一个时间上的循环,将数据拆成 T 个 shape = [N, *] 的数据并逐步输入进去。让我们新建一层IF神经元,设置为单步模式,将数据逐步输入并得到输出:
1 | import torch |
输出结果:
x序列初始化:
1 | x_seq= tensor([[[[[2.5490e-01, 1.2639e-01, 5.7598e-01, 9.8435e-01, 2.7988e-01, |
时间步t=1的情况:
1 | x= tensor([[[[2.5490e-01, 1.2639e-01, 5.7598e-01, 9.8435e-01, 2.7988e-01, |
时间步t=2:
1 | x= tensor([[[[0.2309, 0.9881, 0.1884, 0.2881, 0.0809, 0.4972, 0.4431, 0.4583], |
时间步t=3:
1 | x= tensor([[[[0.8826, 0.4119, 0.6519, 0.2594, 0.5566, 0.8530, 0.5062, 0.3879], |
最终输出的y序列:
1 | y_seq= tensor([[[[[0., 0., 0., 0., 0., 0., 0., 0.], |
multi_step_forward 提供了将 shape = [T, N, *] 的序列数据输入到单步模块进行逐步的前向传播的封装,即将上面的函数进行了封装,使用起来更加方便:
1 | import torch |
但是,直接将模块设置成多步模块,其实更为便捷:
1 | import torch |
测试这两个模式输出的结果是不是相同,下面是代码细节:
1 | #单步模式 |
输出:
1 | y_seq(单步)= tensor([[[[[0., 0., 0., 0., 0., 0., 0., 0.], |
4. 状态保存与重置
SNN中的神经元等模块,与RNN类似,带有隐藏状态,其输出y[t]不仅仅与当前时刻的输入x[t]有关,还与上一个时末的状态h[t-1]有关,即y[t]=f(x[t],h[t-1])。
PyTorch的设计为RNN将状态也一并输出,可以参考torch.nn.RNN的API文档。而在spikingjelly.activation_based中,状态会被保存在模块内部。例如,我们新建一层IF神经元,设置为单步模式,查看给与输入前的默认电压,和给与输入后的电压:
1 | import torch |
在初始化后,IF神经元层的v会被设置为0,首次给与输入后v会自动广播到与输入相同的shape。
若我们给与一个新的输入,则应该先清除神经元之前的状态,让其恢复到初始化状态,可以通过调用模块的self.reset()函数实现:
1 | import torch |
方便起见,还可以通过调用spikingjelly.activation_based.functional.reset_net将整个网络中的所有有状态模块进行重置。
若网络使用了有状态的模块,在训练和推理时,务必在处理完毕一个batch的数据后进行重置:
1 | from spikingjelly.activation_based import functional |
如果忘了重置,在推理时可能输出错误的结果,而在训练时则会直接报错:
1 | RuntimeError: Trying to backward through the graph a second time (or directly access saved variables after they have already been freed). |
5. 传播模式
若一个网络全部由单步模块构成,则整个网络的计算顺序是按照逐步传播(step-by-step)的模式进行,例如:
1 | for t in range(T): |
如果网络全部由多步模块构成,则整个网络的计算顺序是按照逐层传播(layer-by-layer)的模式进行,例如:
1 | import torch |
在绝大多数情况下我们不需要显式的实现 for i in range(net.__len__()) 这样的循环,因为 torch.nn.Sequential 已经帮我们实现过了,因此实际上我们可以这样做:
1 | y_seq_layer_by_layer = net(x_seq) |
逐步传播和逐层传播,实际上只是计算顺序不同,它们的计算结果是完全相同的:
1 | import torch |
上面这段代码的输出为:
1 | net=Sequential( |
下面的图片展示了逐步传播构建计算图的顺序:
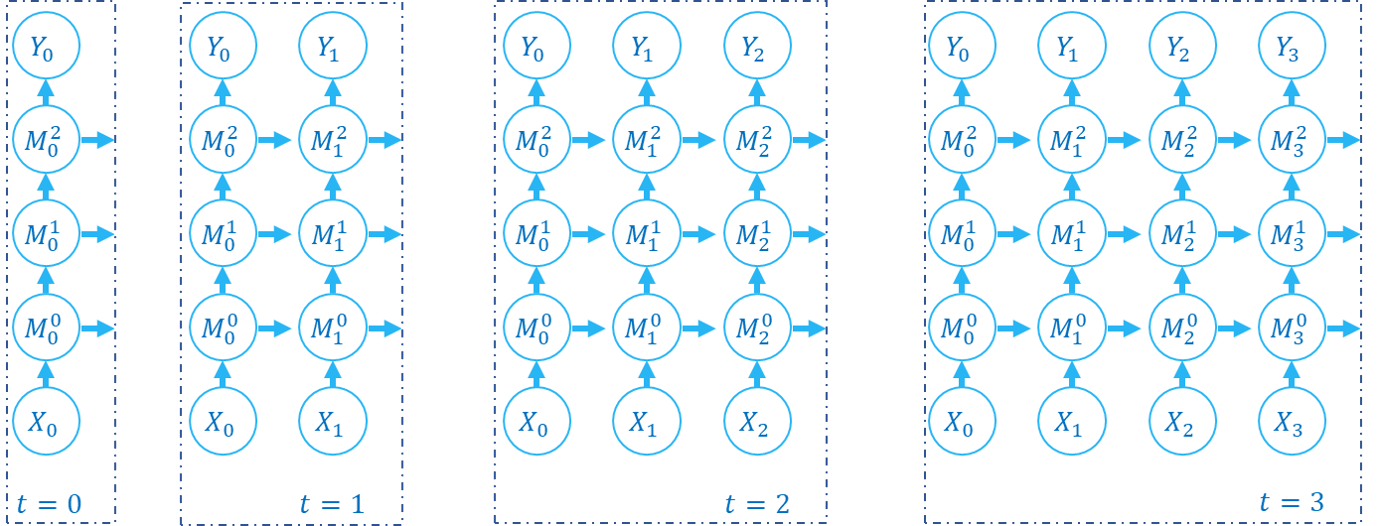
下面的图片展示了逐层传播构建计算图的顺序:
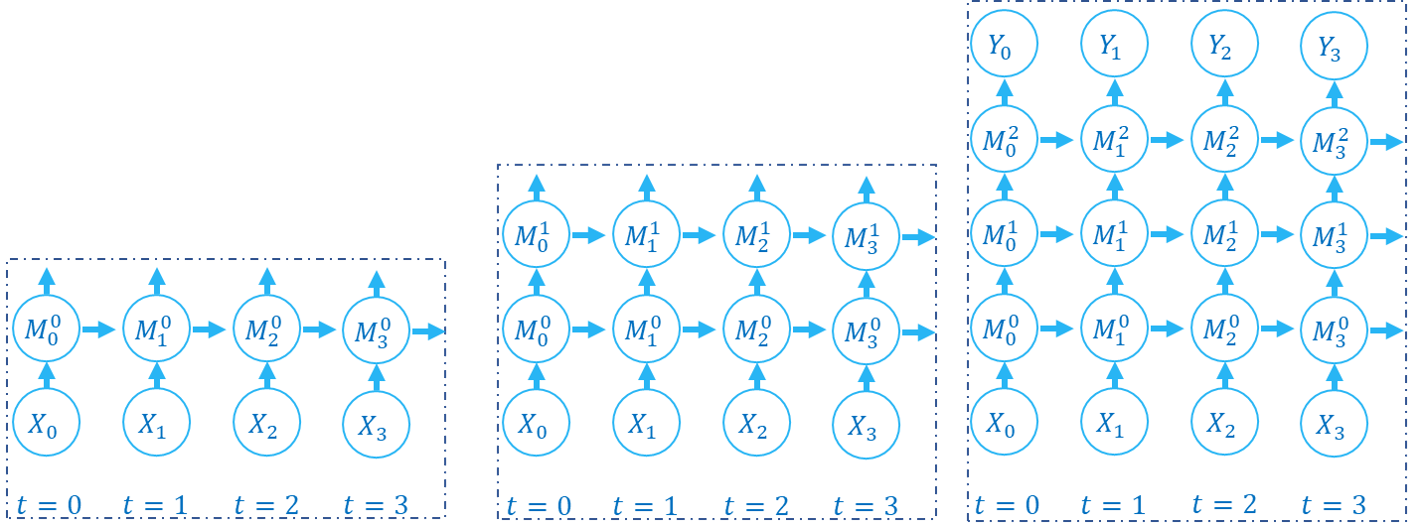
SNN的计算图有2个维度,分别是时间步数和网络深度,网络的传播实际上就是生成完整计算图的过程,正如上面的2张图片所示。实际上,逐步传播是深度优先遍历,而逐层传播是广度优先遍历。
尽管两者区别仅在于计算顺序,但计算速度和内存消耗上会略有区别。
-
在使用梯度替代法训练时,通常推荐使用逐层传播。在正确构建网络的情况下,逐层传播的并行度更大,速度更快
-
在内存受限时使用逐步传播,例如ANN2SNN任务中需要用到非常大的
T。因为在逐层传播模式下,对无状态的层而言,真正的batch size是TN而不是N(参见下一个教程),当T太大时内存消耗极大
