paper

残差网络ResNet

残差网络在设计之初，主要是服务于卷积神经网络(CNN)，在计算机视觉领域应用较多，但是随着CNN结构的发展，在很多文本处理，文本分类里面(n-gram)，也同样展现出来很好的效果。

1.网络深度为什么重要？

我们知道，在CNN网络中，我们输入的是图片的矩阵，也是最基本的特征，整个CNN网络就是一个信息提取的过程，从底层的特征逐渐抽取到高度抽象的特征，网络的层数越多也就意味这能够提取到的不同级别的抽象特征更加丰富，并且越深的网络提取的特征越抽象，就越具有语义信息。


2.为什么不能简单的增加网络层数？

对于传统的CNN网络，简单的增加网络的深度，容易导致梯度消失和爆炸。针对梯度消失和爆炸的解决方法一般是正则初始化(normalized initialization)和中间的正则化层(intermediate normalization layers)，但是这会导致另一个问题，退化问题，随着网络层数的增加，在训练集上的准确率却饱和甚至下降了。这个和过拟合不一样，因为过拟合在训练集上的表现会更加出色。


3.梯度消失和梯度下降

梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。

梯度爆炸：很多大数相乘 梯度消失：很多小于1的数字相乘


4.正则化

在机器学习中，正则化是正则化系数的过程，即对系数进行惩罚，通过向模型添加额外参数来防止模型过度拟合，这有助于提高模型的可靠性、速度和准确性。可以这么说，正则化本质上是为了防止因网络参数过大导致模型过拟合的泛化技术

正则化的作用和意义: 在于防止过度拟合。当发生过拟合时，模型几乎失去了泛化能力。这意味着该模型仅适用于训练它的数据集，而不能被用于其他数据集。

正则化的原理：正则化通过向复杂模型添加带有残差平方和(RSS)的惩罚项来发挥作用

正则化的类型：

  • dropout：在dropout中，激活的随机数会更有效地训练网络。激活是将输入乘以权重时得到的输出。如果在每一层都删除了激活的特定部分，则没有特定的激活会学习输入模型。这意味着输入模型不会出现任何过度拟合。
  • 批量归一化： 批量归一化通过减去批量均值并除以批量标准差来设法归一化前一个激活层的输出。它向每一层引入两个可训练参数，以便标准化输出乘以gamma和beta。gamma和beta的值将通过神经网络找到。通过弱化初始层参数和后面层参数之间的耦合来提高学习率，提高精度，解决协方差漂移问题。
  • 数据扩充：数据扩充涉及使用现有数据创建合成数据，从而增加可用数据的实际数量。通过生成模型在现实世界中可能遇到的数据变化，帮助深度学习模型变得更加精确。
  • 提前停止：使用训练集的一部分作为验证集，并根据该验证集衡量模型的性能。如果此验证集的性能变差，则立即停止对模型的训练。
  • L1正则化：使用L1正则化技术的回归模型称为套索回归。Lasso回归模型即Least Absolute Shrinkage and Selection Operator，将系数的“绝对值”作为惩罚项添加到损失函数中。
  • L2正则化：使用L2正则化的回归模型称为岭回归。岭回归模型即Ridge回归，在Ridge回归中系数的平方幅度作为惩罚项添加到损失函数中。

5.退化问题

按照常理更深层的网络结构的解空间是包括浅层的网络结构的解空间的，也就是说深层的网络结构能够得到更优的解，性能会比浅层网络更佳。但是实际上并非如此，深层网络无论从训练误差或是测试误差来看，都有可能比浅层误差更差，这也证明了并非是由于过拟合的原因。导致这个原因可能是因为随机梯度下降的策略，往往解到的并不是全局最优解，而是局部最优解，由于深层网络的结构更加复杂，所以梯度下降算法得到局部最优解的可能性就会更大。


6.如何解决退化问题

深度网络的退化问题至少说明深度网络不容易训练。但是我们考虑这样一个事实：现在你有一个浅层网络，你想通过向上堆积新层来建立深层网络，一个极端情况是这些增加的层什么也不学习，仅仅复制浅层网络的特征，即这样新层是恒等映射（Identity mapping）。在这种情况下，深层网络应该至少和浅层网络性能一样，也不应该出现退化现象。好吧，你不得不承认肯定是目前的训练方法有问题，才使得深层网络很难去找到一个好的参数。

对于一个堆积层结构（几层堆积而成）当输入为x时其学习特征标记为H(x),现在我们希望其可以学习到残差F(x)=H(x)-x,这样其实原始的学习特征是F(x)+x。之所以这样是因为残差学习相比原始特征直接学习更容易。当残差为0时，此时堆积层仅仅做了恒等映射，至少网络性能不会下降，实际上残差不会为0，这也会使得堆积层在输入特征基础上学习到新的特征，从而拥有更好的性能。


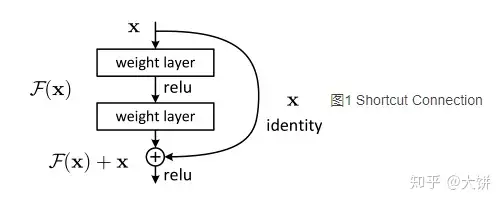
为什么残差学习相对更容易，从直观上看残差学习需要学习的内容少，因为残差一般会比较小，学习难度小点。不过我们可以从数学的角度来分析这个问题，首先残差单元可以表示为:

y1=h(x1)+F(x1,W1)y_1=h(x_1) + F(x_1,W_1)

xl+1=f(y1)x_{l+1}=f(y_1)

  • xl,xl+1x_l,x_{l+1}: 第l个残差单元的输入和输出,每个残差单元包含多层结构
  • F: 残差函数，表示学习到的残差
  • h(x1)=x1h(x_1)=x_1: 表示恒等映射
  • f: RELU激活函数

根据上述，可以得到浅层l到深层L的学习特征为：
xL=xl+∑i=lL−1F(xi,Wi)x_L=x_l + \sum_{i=l}^{L-1}F(x_i,W_i)


根据链式规则，可以求得反向过程梯度：

∂loss∂xl=∂loss∂xL⋅∂xL∂xl=∂loss∂xL⋅(1+∂∑i=lL−1F(xi,Wi)∂xl)\frac{\partial loss}{\partial x_l}=\frac{\partial loss}{\partial x_L}·\frac{\partial x_L}{\partial x_l}=\frac{\partial loss}{\partial x_L}·(1+\frac{\partial \sum_{i=l}^{L-1}F(x_i,W_i)}{\partial x_l})


7.ResNet的tensorflow实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class ResNet50(object):
    def __init__(self, inputs, num_classes=1000, is_training=True,
                 scope="resnet50"):
        self.inputs =inputs
        self.is_training = is_training
        self.num_classes = num_classes

        with tf.variable_scope(scope):
            # construct the model
            net = conv2d(inputs, 64, 7, 2, scope="conv1") # -> [batch, 112, 112, 64]
            net = tf.nn.relu(batch_norm(net, is_training=self.is_training, scope="bn1"))
            net = max_pool(net, 3, 2, scope="maxpool1")  # -> [batch, 56, 56, 64]
            net = self._block(net, 256, 3, init_stride=1, is_training=self.is_training,
                              scope="block2")           # -> [batch, 56, 56, 256]
            net = self._block(net, 512, 4, is_training=self.is_training, scope="block3")
                                                        # -> [batch, 28, 28, 512]
            net = self._block(net, 1024, 6, is_training=self.is_training, scope="block4")
                                                        # -> [batch, 14, 14, 1024]
            net = self._block(net, 2048, 3, is_training=self.is_training, scope="block5")
                                                        # -> [batch, 7, 7, 2048]
            net = avg_pool(net, 7, scope="avgpool5")    # -> [batch, 1, 1, 2048]
            net = tf.squeeze(net, [1, 2], name="SpatialSqueeze") # -> [batch, 2048]
            self.logits = fc(net, self.num_classes, "fc6")       # -> [batch, num_classes]
            self.predictions = tf.nn.softmax(self.logits)


    def _block(self, x, n_out, n, init_stride=2, is_training=True, scope="block"):
        with tf.variable_scope(scope):
            h_out = n_out // 4
            out = self._bottleneck(x, h_out, n_out, stride=init_stride,
                                   is_training=is_training, scope="bottlencek1")
            for i in range(1, n):
                out = self._bottleneck(out, h_out, n_out, is_training=is_training,
                                       scope=("bottlencek%s" % (i + 1)))
            return out

    def _bottleneck(self, x, h_out, n_out, stride=None, is_training=True, scope="bottleneck"):
        """ A residual bottleneck unit"""
        n_in = x.get_shape()[-1]
        if stride is None:
            stride = 1 if n_in == n_out else 2

        with tf.variable_scope(scope):
            h = conv2d(x, h_out, 1, stride=stride, scope="conv_1")
            h = batch_norm(h, is_training=is_training, scope="bn_1")
            h = tf.nn.relu(h)
            h = conv2d(h, h_out, 3, stride=1, scope="conv_2")
            h = batch_norm(h, is_training=is_training, scope="bn_2")
            h = tf.nn.relu(h)
            h = conv2d(h, n_out, 1, stride=1, scope="conv_3")
            h = batch_norm(h, is_training=is_training, scope="bn_3")

            if n_in != n_out:
                shortcut = conv2d(x, n_out, 1, stride=stride, scope="conv_4")
                shortcut = batch_norm(shortcut, is_training=is_training, scope="bn_4")
            else:
                shortcut = x
            return tf.nn.relu(shortcut + h)